Exam 13: Inference in Linear Models
Exam 1: Basic Ideas39 Questions
Exam 2: Graphical Summaries of Data40 Questions
Exam 3: Numerical Summaries of Data76 Questions
Exam 4: Summarizing Bivariate Data33 Questions
Exam 5: Probability99 Questions
Exam 6: Discrete Probability Distributions76 Questions
Exam 7: The Normal Distribution131 Questions
Exam 8: Confidence Intervals62 Questions
Exam 9: Hypothesis Testing115 Questions
Exam 10: Two-Sample Confidence Intervals44 Questions
Exam 11: Two-Sample Hypothesis Tests43 Questions
Exam 12: Tests With Qualitative Data26 Questions
Exam 13: Inference in Linear Models51 Questions
Exam 14: Analysis of Variance48 Questions
Exam 15: Nonparametric Statistics27 Questions
Select questions type
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
Visual Auditory 185 244 204 244 242 247 209 245 191 243 250 249 155 237 188 245
Compute a point estimate for the mean auditory response time for subjects with a visual response time of .
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
B
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
Visual Auditory 166 241 192 242 242 250 188 244 232 252 240 254 197 245 203 247
Predict the auditory response time for a particular subject whose visual response time of 178.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
B
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of a second. The results are presented in the following table.
Visual Auditory 168 243 233 253 169 242 204 243 206 248 202 245 157 239 240 248
i). Compute a point estimate for the mean auditory response time for subjects with a visual response time of 183.
ii). Construct a 99% confidence interval for the mean auditory response time for subjects with a visual response time of 183.
iii). Predict the auditory response time for a particular subject whose visual response time of 183.
iv). Construct a 99% prediction interval for the auditory response time for a particular subject whose visual response time is 183.
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
i). 243.34
ii). (239.85, 246.83)
iii). 243.34
iv). (233.86, 252.82)
The following display from a TI-84 Plus calculator presents the results of a test of the null hypothesis .
 What is the value of the test statistic?
What is the value of the test statistic?
(Multiple Choice)
4.8/5  (40)
(40)
The summary statistics for a certain set of points are: , and Assume the conditions of the linear model hold. A 95% confidence interval for will be constructed.
Construct the 95% confidence interval.
(Multiple Choice)
4.8/5  (34)
(34)
The following MINITAB output presents a multiple regression equatior =b0+b1x1+b2x2+b3x3+b4x4
The regression equation is
Predictor Coef SE Coef T Constant 4.7712 0.7648 0.92800 0.3280 1 0.2662 0.8036 -0.93740 0.3570 2 1.2710 0.8451 1.74170 0.0830 3 -1.1349 0.6318 -2.94990 0.0080 4 -1.8545 0.6753 3.27200 0.0020
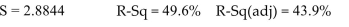 Source DF SS MS F P Regression 4 624.2 156.1 9.8797 0.003 Residual Error 40 633.7 15.8 Total 44 1,257.9
It is desired to drop one of the explanatory variables. Which of the following is the most appropriate action?
Source DF SS MS F P Regression 4 624.2 156.1 9.8797 0.003 Residual Error 40 633.7 15.8 Total 44 1,257.9
It is desired to drop one of the explanatory variables. Which of the following is the most appropriate action?
(Multiple Choice)
4.8/5  (40)
(40)
The summary statistics for a certain set of points are: , and . Assume the conditions of the linear model hold. A confidence interval for will be constructed. What is the margin of error?
(Multiple Choice)
4.8/5  (33)
(33)
Use the given set of points to construct a confidence interval for the mean response for the given value of .
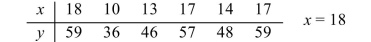
(Multiple Choice)
4.8/5  (40)
(40)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths
Of a second. The results are presented in the following table.
Visual Auditory 208 249 200 244 245 254 234 249 155 243 211 248 189 244 206 247
Test H0: =0 versus . Use the :=0.05 level of significance.
(Multiple Choice)
4.8/5  (34)
(34)
The following display from a TI-84 Plus calculator presents the results of a test of the null hypothesis
 Can you conclude that the explanatory variable is useful in predicting the outcome variable? Answer this question using the level of significance.
Can you conclude that the explanatory variable is useful in predicting the outcome variable? Answer this question using the level of significance.
(True/False)
4.8/5  (28)
(28)
The following display from a TI-84 Plus calculator presents the results of a test of the null hypothesis .
 What is the P-value?
What is the P-value?
(Multiple Choice)
4.8/5  (36)
(36)
For a sample of size 15 , the following values were obtained: , , and
Construct a confidence interval for the mean response when .
(Multiple Choice)
4.9/5  (37)
(37)
The summary statistics for a certain set of points are: , and . Assume the conditions of the linear model hold. A confidence interval for will be constructed. How many degrees of freedom are there for the critical value?
(Multiple Choice)
4.9/5  (30)
(30)
Use the given set of points to
a). Compute and .
b). Compute the predicted value for the given value of x.
c). Compute the residual standard deviation
d). Compute the sum of squares for
e). Find the critical value for a 95% confidence or prediction interval.
f). Construct a 95% confidence interval for the mean response for the given value of x.
g). Construct a 95% prediction interval for an individual response for the given value of x.
x 12 10 19 15 11 15 y 31 28 46 39 31 37 xequals16
(Short Answer)
4.7/5  (37)
(37)
The summary statistics for a certain set of points are: n=10, se=3.199, =11.257, and =1.704 . Assume the conditions of the linear model hold. A 99% confidence interval for will be constructed.
i). How many degrees of freedom are there for the critical value?
ii). What is the critical value?
iii). What is the margin of error?
iv). Construct the 99% confidence interval.
(Short Answer)
4.8/5  (36)
(36)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 6 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
The following MINITAB output describes the fit of a linear model to these data. Assume that the assumptions Of the linear model are satisfied.
The regression equation is Auditory Visual
Predictor Coef SE Coef T P Constant 169.803813 17.123244 9.916568 0.000581 Visual 0.4671 0.081367 5.740635 0.004563
What is the slope of the least-squares regression line?
(Multiple Choice)
4.8/5  (33)
(33)
The following MINITAB output presents a confidence interval for a mean response and a prediction interval for an individual response. 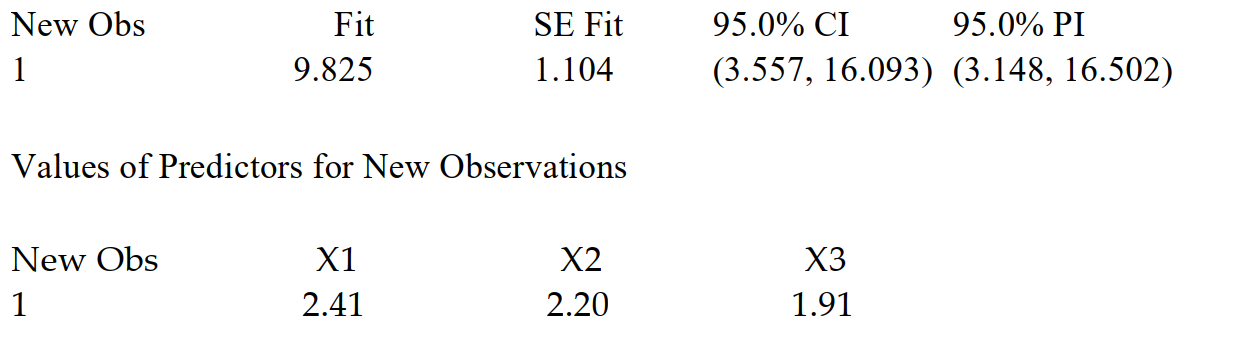 What is the prediction interval for the new observation?
What is the prediction interval for the new observation?
(Short Answer)
4.8/5  (41)
(41)
The following MINITAB output presents a 95% confidence interval for the mean ozone level on days when the relative humidity is 40%, and a 95% prediction interval for the ozone level on a Particular day when the relative humidity is 40%. The units of ozone are parts per billion. Predicted Values for New Observations
New Obs Fit SE Fit 95.0\% CI 95.0\% PI 1 38.37 1.3 (35.82,40.92) (21.16,55.58)
Values of Predictors for New Observations
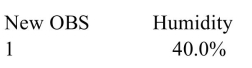 Predict the ozone level for a day when the relative humidity is 40%.
Predict the ozone level for a day when the relative humidity is 40%.
(Multiple Choice)
4.8/5  (40)
(40)
The following MINITAB output presents a multiple regression equatior =b0+b1x1+b2x2+b3x3+b4x4
The regression equation is
Predictor Coef SE Coef T P Constant 5.5079 0.7640 1.1002 0.314 X1 1.6552 0.7032 3.1929 0.002 X2 -1.1088 0.6023 -3.2310 0.005 X3 1.3981 0.8970 1.8137 0.087 X4 -1.2465 0.8251 -1.1433 0.354
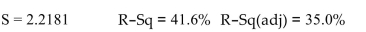 Source DF SS MS F P Regression 4 637.5 159.4 7.1480 0.003 Residual Error 40 893.2 22.3 Total 44 1,530.7
Let be the coefficient Test the hypothesis rersus
level. What do you conclude?
Source DF SS MS F P Regression 4 637.5 159.4 7.1480 0.003 Residual Error 40 893.2 22.3 Total 44 1,530.7
Let be the coefficient Test the hypothesis rersus
level. What do you conclude?
(Multiple Choice)
4.8/5  (42)
(42)
Use the given set of points to
a). Compute b1.
b). Compute the residual standard deviation se.
c). Compute the sum of squares for x,
d). Compute the standard error of b1, sb.
e). Find the critical value for a 95% confidence interval for
f). Compute the margin of error for a 95% confidence interval for
g). Construct a 95% confidence interval for
h). Test the null hypothesis versus Use the =0.05 level of significance.
x 8 11 15 13 6 8 12 13 y 23 27 37 33 17 20 29 36
(Short Answer)
4.9/5  (33)
(33)
Showing 1 - 20 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)