Exam 10: Two-Sample Confidence Intervals

Using technology, solve the following problem: A survey of college students reported that in a sample of 442 male students, the average number of energy drinks consumed per month was 2.39 With a standard deviation of 4.92, and in a sample of 77 female students, the average was 1.53 with A standard deviation of 3.07. Construct a 90% confidence interval for the difference between men and women in the mean number Of energy drinks consumed.

Two microprocessors are compared on a sample of 6 benchmark codes to determine whether there is a difference in speed. The times (in seconds) used by each processor on each code are given below: 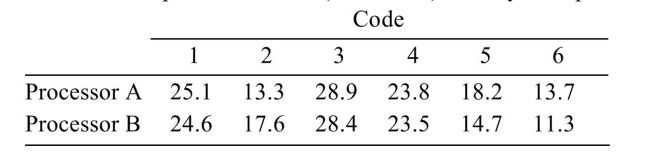An electronics engineer claims that the mean speed is the same for both processors. Does The 99% confidence interval contradict this claim? (Hint: First find the 99% confidence interval for The difference between the mean speeds.)

Traffic engineers compared rates of traffic collisions at intersections with raised medians and rates at intersections with two-way left-turn lanes. They found that out of 4,653 collisions at intersections With raised medians, 2,289 were rear-end collisions, and out of 4,606 collisions at two-way left-turn Lanes, 2,027 were rear-end collisions. Assuming these to be random samples of collisions from the two types of intersections, construct a 95% Confidence interval for the difference between the proportions of collisions that are of the rear-end Type at the two types of intersection.

The following MINITAB output display presents a 95% confidence interval for the difference between two proportions. Sample Sample P 1 29 628 0.046178 2 106 625 0.169600 Difference $= p ( 1 ) - p ( 2 )$ Estimate for difference: $- 0.123422$ $95 \%$ CI for difference: $( - 0.152 , - 0.095 )$ What is the point estimate of $p _ { 1 } - p _ { 2 }$ ?