Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 10: Analytical Geometry

arrow
Exam 1: Line and Angle Relationships13 Questionsadd course
Exam 2: Parallel Lines13 Questionsadd course
Exam 3: Triangles16 Questionsadd course
Exam 4: Quadrilaterals14 Questionsadd course
Exam 5: Similar Triangles12 Questionsadd course
Exam 6: Circles10 Questionsadd course
Exam 7: Locus and Concurrence4 Questionsadd course
Exam 8: Areas of Polygons and Circles5 Questionsadd course
Exam 9: Surfaces and Solids4 Questionsadd course
Exam 10: Analytical Geometry8 Questionsadd course
Exam 11: Introduction to Trigonometry4 Questionsadd course
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

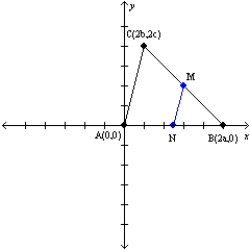-Let a, b, and c represent positive real numbers. Use the drawing in which the vertices of are A(0,0), B(2a,0), and C(2b,2c) to prove the following theorem. The line segment determined by the midpoints of two sides of a triangle is parallel to the third side of the triangle. -Let a, b, and c represent positive real numbers. Use the drawing in which the vertices of -Let a, b, and c represent positive real numbers. Use the drawing in which the vertices of 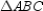are A(0,0), B(2a,0), and C(2b,2c) to prove the following theorem. The line segment determined by the midpoints of two sides of a triangle is parallel to the third side of the triangle. are A(0,0), B(2a,0), and C(2b,2c) to prove the following theorem. "The line segment determined by the midpoints of two sides of a triangle is parallel to the third side of the triangle."

Free
(Essay)
4.9/5
(22)
Question 1
Correct Answer:
Verified

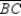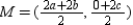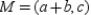With M the midpoint of With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . , we have With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . so With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . . Where N is
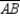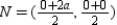the midpoint of With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . , With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . so With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . . Then With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . .
Also, With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . . Because With M the midpoint of , we have so . Where N is the midpoint of , so 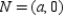. Then 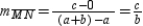. Also, 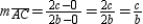. Because , it follows that . , it follows that 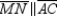With M the midpoint of , we have so . Where N is the midpoint of , so . Then . Also, . Because , it follows that . .

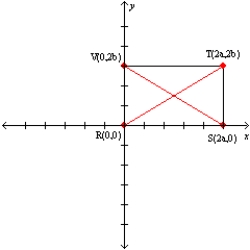-Let a and b represent positive real numbers. Use the drawing in which the vertices of rectangle RSTV are R(0,0), S(2a,0), T(2a,2b), and V(0,2b) to prove the following theorem. The diagonals of a rectangle bisect each other. -Let a and b represent positive real numbers. Use the drawing in which the vertices of rectangle RSTV are R(0,0), S(2a,0), T(2a,2b), and V(0,2b) to prove the following theorem. "The diagonals of a rectangle bisect each other."

Free
(Essay)
4.8/5
(42)
Question 2
Correct Answer:
Verified

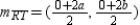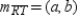To complete the proof, we show that the midpoint of diagonal To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. and the midpoint of diagonal To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. are the same point, namely the point of intersection of these diagonals.
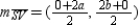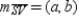Now To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. so To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. . Also, To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. so To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. .
Thus, the common midpoint of To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. and To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. must be their point of intersection, so To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. and To complete the proof, we show that the midpoint of diagonal and the midpoint of diagonal are the same point, namely the point of intersection of these diagonals. Now so . Also, so . Thus, the common midpoint of and must be their point of intersection, so and bisect each other. bisect each other.

-Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that . [Note: No drawing provided.] -Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that -Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that . [Note: No drawing provided.] . [Note: No drawing provided.]

Free
(Essay)
4.9/5
(36)
Question 3
Correct Answer:
Verified

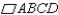For ABCD to represent a rhombus, the lengths of 2 adjacent sides of For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . Thus, ABCD is a rhombus when . must be congruent. Of course, For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . 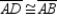Thus, ABCD is a rhombus when . 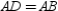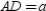when For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . Thus, ABCD is a rhombus when . . 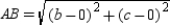With A and D on the x axis, we see that For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . Thus, ABCD is a rhombus when . . Applying the Distance Formula, we also have For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . Thus, ABCD is a rhombus when . or For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or . Thus, ABCD is a rhombus when . .
Thus, ABCD is a rhombus when For ABCD to represent a rhombus, the lengths of 2 adjacent sides of must be congruent. Of course, when . With A and D on the x axis, we see that . Applying the Distance Formula, we also have or 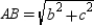. Thus, ABCD is a rhombus when . .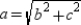

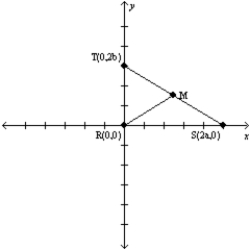-Let a and b represent positive real numbers. Use the right triangle with vertices at R(0,0), S(2a,0), and T(0,2b) to prove the following theorem. The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices of the triangle. -Let a and b represent positive real numbers. Use the right triangle -Let a and b represent positive real numbers. Use the right triangle 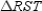with vertices at R(0,0), S(2a,0), and T(0,2b) to prove the following theorem. The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices of the triangle. with vertices at R(0,0), S(2a,0), and T(0,2b) to prove the following theorem. "The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices of the triangle."

(Essay)
4.7/5
(40)
Question 4

-Let a and b represent positive real numbers. Explain why the triangle with vertices at A(a,0), B(0,a) and C(0,0) is an isosceles right triangle. -Let a and b represent positive real numbers. Explain why the triangle with vertices at A(a,0), B(0,a) and C(0,0) is an isosceles right triangle.

(Essay)
4.8/5
(38)
Question 5

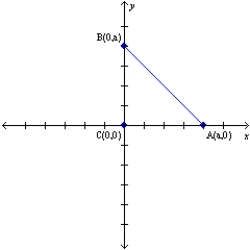
-Let a, b, and c represent positive real numbers. Given that quadrilateral ABCD has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c), explain why ABCD must be a parallelogram. -Let a, b, and c represent positive real numbers. Given that quadrilateral ABCD has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c), explain why ABCD must be a parallelogram.

(Essay)
4.8/5
(31)
Question 6

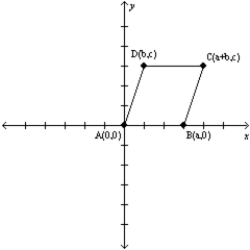
-Let a, b, and c represent positive real numbers. Given the rhombus ABCD with vertices at A(0,0), B(a,0), C(a+b,c) and D(b,c), prove the following theorem. The diagonals of a rhombus are perpendicular. -Let a, b, and c represent positive real numbers. Given the rhombus ABCD with vertices at A(0,0), B(a,0), C(a+b,c) and D(b,c), prove the following theorem. "The diagonals of a rhombus are perpendicular."

(Essay)
4.8/5
(31)
Question 7

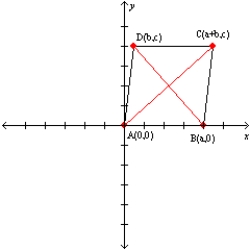-Let a, b, and c represent positive real numbers. Use the figure in which has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem. If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle. -Let a, b, and c represent positive real numbers. Use the figure in which -Let a, b, and c represent positive real numbers. Use the figure in which has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem. If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle. has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem. "If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle."

(Essay)
4.7/5
(36)
Question 8
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)