Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 5: Similar Triangles

arrow
Exam 1: Line and Angle Relationships13 Questionsadd course
Exam 2: Parallel Lines13 Questionsadd course
Exam 3: Triangles16 Questionsadd course
Exam 4: Quadrilaterals14 Questionsadd course
Exam 5: Similar Triangles12 Questionsadd course
Exam 6: Circles10 Questionsadd course
Exam 7: Locus and Concurrence4 Questionsadd course
Exam 8: Areas of Polygons and Circles5 Questionsadd course
Exam 9: Surfaces and Solids4 Questionsadd course
Exam 10: Analytical Geometry8 Questionsadd course
Exam 11: Introduction to Trigonometry4 Questionsadd course
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

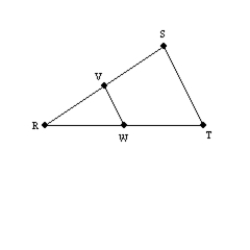-Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. -Supply missing statements and missing reasons for the following proof. Given: -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. 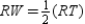; V is the midpoint of -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. 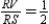and W is the midpoint of -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. . 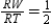Prove: -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. S1. R1. S2. -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. and -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. R2. Definition of midpoint S3. -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. and -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. R5. S6. R6. R3. S4. R4. Substitution Property of Equality S5. -Supply missing statements and missing reasons for the following proof. Given: ; V is the midpoint of and W is the midpoint of . Prove: S1. R1. S2. and R2. Definition of midpoint S3. and R3. S4. R4. Substitution Property of Equality S5. 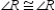R5. S6. R6. R5. S6. R6.

Free
(Essay)
5.0/5
(38)
Question 1
Correct Answer:
Verified

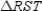S1. S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. R5. Identity S6. R6. SAS ; V is the midpoint of S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. R5. Identity S6. R6. SAS and W is the midpoint of S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. R5. Identity S6. R6. SAS .
R1. Given
R3. Division Property of Equality
S4. S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. R5. Identity S6. R6. SAS R5. Identity
S6. S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. R5. Identity S6. R6. SAS R6. SAS S1. ; V is the midpoint of and W is the midpoint of . R1. Given R3. Division Property of Equality S4. 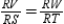R5. Identity S6. 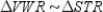R6. SAS

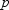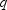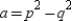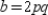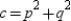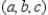Where Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. and Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. are natural numbers and Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. , let Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. , Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. , and Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. . Verify that Where and are natural numbers and , let , , and . Verify that is a Pythagorean Triple. is a Pythagorean Triple.

Free
(Essay)
4.7/5
(44)
Question 2
Correct Answer:
Verified

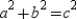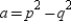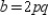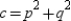We need to show that We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . . Where We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . , We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 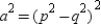, and We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 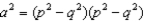, it follws that We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 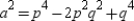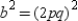or We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 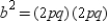, so that We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 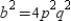, We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 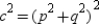or We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 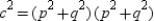, so that We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 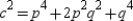, and We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 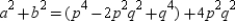or We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . 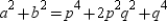, so that We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . .
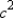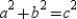Now We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . or We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . , which is the
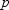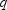value of We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . . That is, We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . for all choices of We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . and We need to show that . Where , , and , it follws that or , so that , or , so that , and or , so that . Now or , which is the value of . That is, for all choices of and . .

-Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. -Supply missing statements and missing reasons for for the following proof. Given: -Supply missing statements and missing reasons for for the following proof. Given: ; 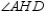and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. 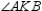; -Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. 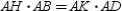and -Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. 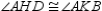are right angles Prove: -Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. S1. R1. S2. 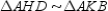-Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. R2. S3. R3.Opposite angles of a parallelogram. S4. -Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. R4. S5. -Supply missing statements and missing reasons for for the following proof. Given: ; and are right angles Prove: S1. R1. S2. R2. S3. R3.Opposite angles of a parallelogram. S4. R4. S5. 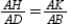R5. S6. R6. In a proportion, the product of the means equals the product of the extremes. R5. S6. R6. In a proportion, the product of the means equals the product of the extremes.

Free
(Essay)
4.9/5
(36)
Question 3
Correct Answer:
Verified

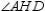S1. S1. ; and are right angles R1. Given R2. All right angles are congruent S3. R4. AA R5. CSSTP S6. ; S1. ; and are right angles R1. Given R2. All right angles are congruent S3. R4. AA R5. CSSTP S6. and S1. ; and are right angles R1. Given R2. All right angles are congruent S3. R4. AA R5. CSSTP S6. are right angles
R1. Given
R2. All right angles are congruent
S3. S1. ; and are right angles R1. Given R2. All right angles are congruent S3. R4. AA R5. CSSTP S6. R4. AA
R5. CSSTP
S6. S1. ; and 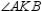are right angles R1. Given R2. All right angles are congruent S3. 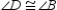R4. AA R5. CSSTP S6.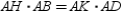

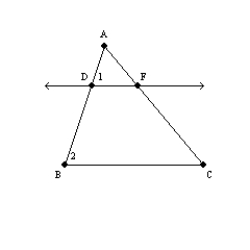-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality -Supply the missing reasons for the following proof. Given: -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. 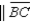Substitution Property of Equality and -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. 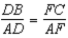Substitution Property of Equality -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. 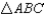Substitution Property of Equality Prove: -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality S1. 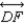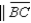-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. 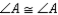Substitution Property of Equality and -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. 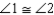Substitution Property of Equality -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R1. S2. 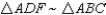-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R2. S3. 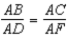-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R3. S4. 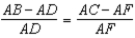-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R4. S5. 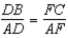-Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R5. S6. -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R6. A property of proportions S7. -Supply the missing reasons for the following proof. Given: and Prove: S1. and R1. S2. R2. S3. R3. S4. R4. S5. R5. S6. R6. A property of proportions S7. R7. Substitution Property of Equality R7. Substitution Property of Equality

(Essay)
4.8/5
(37)
Question 4

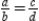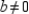Explain (prove) the following property of proportions. "If Explain (prove) the following property of proportions. If (where and ), then . (where Explain (prove) the following property of proportions. If (where and ), then . and Explain (prove) the following property of proportions. If (where and ), then . ), then Explain (prove) the following property of proportions. If (where and 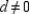), then . ."

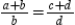(Essay)
4.8/5
(27)
Question 5

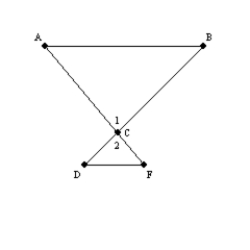-Supply missing statements and missing reasons in the following proof. Given: in the figure shown Prove: S1. R1. S2. R2. S3. R3. Vertical angles are congruent. S4. R4. -Supply missing statements and missing reasons in the following proof. Given: -Supply missing statements and missing reasons in the following proof. Given: 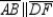in the figure shown Prove: S1. R1. S2. R2. S3. R3. Vertical angles are congruent. S4. R4. 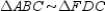in the figure shown Prove: -Supply missing statements and missing reasons in the following proof. Given: in the figure shown Prove: S1. R1. S2. R2. S3. R3. Vertical angles are congruent. S4. R4. S1. R1. S2. -Supply missing statements and missing reasons in the following proof. Given: in the figure shown Prove: S1. R1. S2. 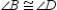R2. S3. R3. Vertical angles are congruent. S4. R4. R2. S3. R3. Vertical angles are congruent. S4. R4.

(Essay)
4.8/5
(43)
Question 6

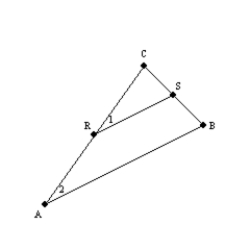-Provide all statements and all reasons for this proof. Given: with Prove: -Provide all statements and all reasons for this proof. Given: -Provide all statements and all reasons for this proof. Given: 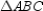with Prove: with -Provide all statements and all reasons for this proof. Given: with Prove: Prove: -Provide all statements and all reasons for this proof. Given: with 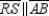Prove: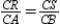

(Essay)
4.7/5
(35)
Question 7

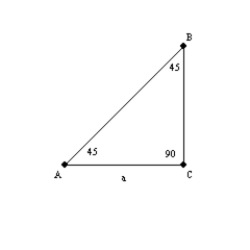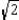-Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. Given: with , , and Prove: and -Use the drawing provided to explain the 45 -45 -90 Theorem. "In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. 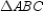Given: with , , and Prove: and and the length of either leg." Given: -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. 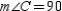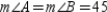Given: with , , and Prove: and with -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. 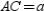Given: with , , and Prove: and , -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. 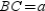Given: with , , and Prove: and , and -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. 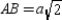Given: with , , and Prove: and Prove: -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. Given: with , , and Prove: and and -Use the drawing provided to explain the 45 -45 -90 Theorem. In a triangle whose angles measure 45 , 45 , and 90 , the hypotenuse has a length equal to the product of and the length of either leg. Given: with , , and Prove: and

(Essay)
4.9/5
(29)
Question 8

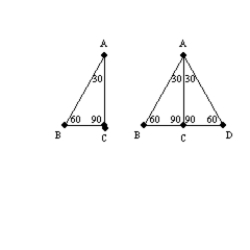-Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. Given: Right with , , and ; also, Prove: and -Use the drawing(s) to explain the 30 -60 -90 Theorem. 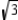"In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 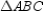Given: Right with , , and ; also, Prove: and and the length of the shorter leg." Given: Right -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 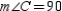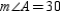Given: Right with , , and ; also, Prove: and with -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 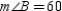Given: Right with , , and ; also, Prove: and , -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 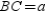Given: Right with , , and ; also, Prove: and , and -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 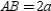Given: Right with , , and ; also, Prove: and ; also, -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. 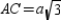Given: Right with , , and ; also, Prove: and Prove: -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. Given: Right with , , and ; also, Prove: and and -Use the drawing(s) to explain the 30 -60 -90 Theorem. In a triangle whose angles measure 30 , 60 , and 90 , the hypotenuse has a length equal to twice the length of the shorter leg, and the length of the longer leg is the product of and the length of the shorter leg. Given: Right with , , and ; also, Prove: and

(Essay)
4.9/5
(29)
Question 9

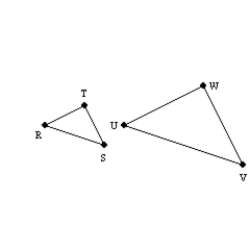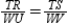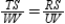-Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. CASTC -Provide the missing statements and missing reasons for the following proof. Given: -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. CASTC and -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. 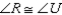CASTC ; -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. 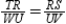CASTC and -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. CASTC Prove: -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. CASTC S1. R1. Given S2. -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. R3. S4. R4. CASTC R2. S3. -Provide the missing statements and missing reasons for the following proof. Given: and ; and Prove: S1. R1. Given S2. R2. S3. 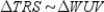R3. S4. R4. CASTC R3. S4. R4. CASTC

(Essay)
4.9/5
(38)
Question 10

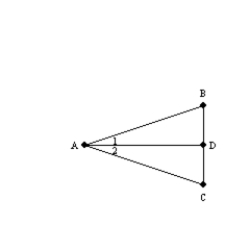-Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. -Supply missing statements and missing reasons for the following proof. Given: -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 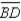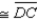; -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 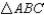bisects -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 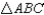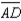and -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 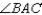-Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 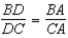Prove: -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. is an isosceles triangle S1. 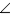-Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 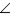; -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. bisects -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. R1. S2. -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. R2. If a ray bisects one -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. of a -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. . S3. R3. Given S4. 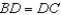-Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. R4. S5. 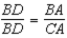-Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. 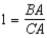, so -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. R6. S7. R7. R5. S6. -Supply missing statements and missing reasons for the following proof. Given: ; bisects and Prove: is an isosceles triangle S1. ; bisects R1. S2. R2. If a ray bisects one of a , it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected . S3. R3. Given S4. R4. S5. , so R5. S6. 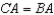R6. S7. R7. R6. S7. R7.

(Essay)
4.8/5
(31)
Question 11

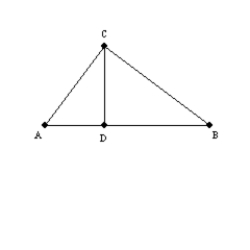-Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. -Supply missing statements and missing reasons for the proof of this theorem. "The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other." Given: Right triangle ABC with rt. -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. 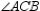; 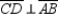Prove: 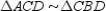S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. 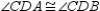; -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. 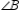Prove: -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. S1. R1. S2. 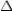-Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. R2. S3. 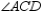-Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. and -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. are comp. R3. The acute angles of a rt. -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. are comp. S4. -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. and -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. are comp. R4. S5. R5. If 2 -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. s are comp. to the same -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. , these -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are . S6. R6. are -Supply missing statements and missing reasons for the proof of this theorem. The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two right triangles that are similar to each other. Given: Right triangle ABC with rt. ; Prove: S1. R1. S2. R2. S3. and are comp. R3. The acute angles of a rt. are comp. S4. and are comp. R4. S5. R5. If 2 s are comp. to the same , these are 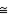. S6. R6. . S6. R6.

(Essay)
4.9/5
(41)
Question 12
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)