Exam 4: Quadrilaterals
Exam 1: Line and Angle Relationships13 Questions
Exam 2: Parallel Lines13 Questions
Exam 3: Triangles16 Questions
Exam 4: Quadrilaterals14 Questions
Exam 5: Similar Triangles12 Questions
Exam 6: Circles10 Questions
Exam 7: Locus and Concurrence4 Questions
Exam 8: Areas of Polygons and Circles5 Questions
Exam 9: Surfaces and Solids4 Questions
Exam 10: Analytical Geometry8 Questions
Exam 11: Introduction to Trigonometry4 Questions
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questions
Select questions type
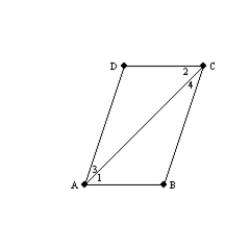
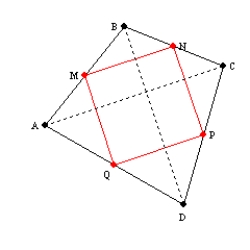 -In quadrilateral ABCD, the midpoints of the sides are joined in order.
Use the auxiliary diagonals to explain why the resulting quadrilateral MNPQ must be a parallelogram.
-In quadrilateral ABCD, the midpoints of the sides are joined in order.
Use the auxiliary diagonals to explain why the resulting quadrilateral MNPQ must be a parallelogram.
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
The line segements that join midpoints of 2 sides of a triangle are parallel to the third side of the triangle. For this reason, 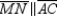 in
in 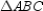 and
and 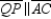 in
in 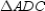 ; thus, it follows
; thus, it follows
that 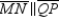 . Similarly,
. Similarly, 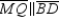 in
in 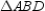 and
and 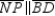 in
in  ; thus,
; thus, 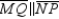 .
.
By definition, it follows that MNPQ is a parallelogram.
 -Provide missing reasons for the proof of the theorem, "A diagonal of a parallelogram separates it into two congruent triangles."
Given:
-Provide missing reasons for the proof of the theorem, "A diagonal of a parallelogram separates it into two congruent triangles."
Given: 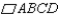 with diagonal
with diagonal 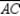 Prove:
Prove: 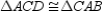 S1.
S1. 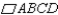 with diagonal
with diagonal 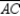 R1.
S2.
R1.
S2. 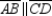 R2.
S3.
R2.
S3. 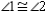 R3.
S4.
R3.
S4. 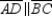 R4.
S5.
R4.
S5. 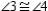 R5.
S6.
R5.
S6. 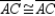 R6.
S7.
R6.
S7. 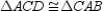 R7.
R7.
Free
(Essay)
4.9/5  (39)
(39)
Correct Answer:
R1. Given
R2. The opposite sides of a parallelogram are parallel (definition).
R3. If 2 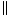 lines are cut by a trans, the alternate interior angles are congruent.
lines are cut by a trans, the alternate interior angles are congruent.
R4. Same as reason 2
R5. Same as reason 3.
R6. Identity
R7. ASA
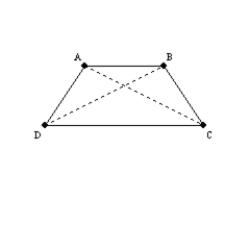 -Suppose that you have already proved that "The diagonals of an isosceles trapezoid are congruent." Use this theorem to prove that "A pair of base angles of an isosceles trapezoid are congruent." Supply missing statements and missing reasons for the proof.
Given: Trapezoid ABCD;
-Suppose that you have already proved that "The diagonals of an isosceles trapezoid are congruent." Use this theorem to prove that "A pair of base angles of an isosceles trapezoid are congruent." Supply missing statements and missing reasons for the proof.
Given: Trapezoid ABCD; 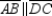 and
and 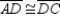 Prove:
Prove: 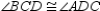 S1. R1.
S2. Draw
S1. R1.
S2. Draw 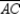 and
and 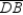 R2.
S3.
R2.
S3. 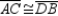 R3.
S4. R4. Identity
S5.
R3.
S4. R4. Identity
S5. 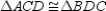 R5.
S6.
R5.
S6. 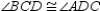 R6.
R6.
Free
(Essay)
4.9/5  (31)
(31)
Correct Answer:
S1. Trapezoid ABCD; 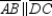 and
and 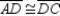 R1. Given
R1. Given
R2. Through 2 points, there is exactly one line.
R3. The diagonals of an isosceles trapezoid are congruent.
S4. 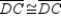 R5. SSS
R5. SSS
R6. CPCTC
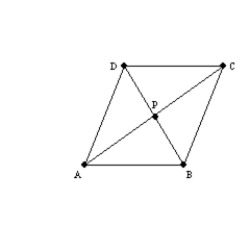 -Provide missing statements and missing reasons for the following proof.
Given:
-Provide missing statements and missing reasons for the following proof.
Given:  ; diagonals
; diagonals  and
and  intersect at point P
Prove:
intersect at point P
Prove: 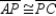 and
and 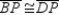 S1. R1. Given
S2.
S1. R1. Given
S2. 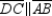 R2.
S3.
R2.
S3. 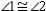 and
and 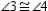 R3.
S4.
R3.
S4. 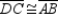 R4.
S5. R5. ASA
S6. R6.
R4.
S5. R5. ASA
S6. R6.
(Essay)
4.8/5  (28)
(28)
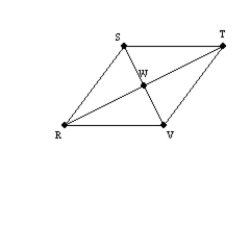 -Given the rhombus RSTV, diagonals
-Given the rhombus RSTV, diagonals  and
and  intersect at point W. Explain why it follows that
intersect at point W. Explain why it follows that 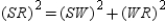 .
.
(Essay)
4.8/5  (28)
(28)
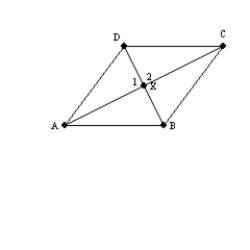 -Provide missing statements and missing reasons for the proof of the following theorem.
"The diagonals of a rhombus are perpendicular."
Given: Rhombus ABCD; diagonals
-Provide missing statements and missing reasons for the proof of the following theorem.
"The diagonals of a rhombus are perpendicular."
Given: Rhombus ABCD; diagonals 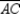 and
and 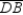 intersect at point X
Prove:
intersect at point X
Prove: 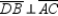 S1. R1.
S2.
S1. R1.
S2. 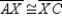 R2. The diagonals of a rhombus (
R2. The diagonals of a rhombus (  ) bisect each other.
S3.
) bisect each other.
S3. 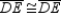 R3.
S4. R4. All sides of a rhombus are congruent.
S5. R5. SSS
S6.
R3.
S4. R4. All sides of a rhombus are congruent.
S5. R5. SSS
S6. 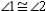 R6.
S7. R7.
R6.
S7. R7.
(Essay)
4.7/5  (42)
(42)
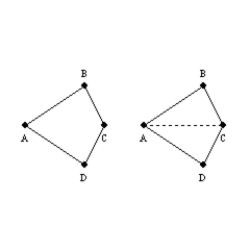 -Provide missing statements and missing reasons for the proof of this theorem.
"In a kite, one pair of opposite angles are congruent."
Given: Kite ABCD with
-Provide missing statements and missing reasons for the proof of this theorem.
"In a kite, one pair of opposite angles are congruent."
Given: Kite ABCD with 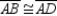 and
and 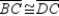 Prove:
Prove: 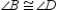 S1. R1.
S2. Draw
S1. R1.
S2. Draw 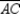 R2.
S3.
R2.
S3. 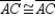 R3.
S4. R4. SSS
S5. R5.
R3.
S4. R4. SSS
S5. R5.
(Essay)
4.8/5  (36)
(36)
 -Provide all statements and all reasons for the following proof.
Given:
-Provide all statements and all reasons for the following proof.
Given:  ,
,  ,
, 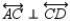 , and
, and 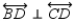 Prove: Quad. ABCD is a parallelogram
Prove: Quad. ABCD is a parallelogram
(Essay)
4.7/5  (33)
(33)
![-Use the drawing shown to explain the following theorem. The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases. Given: Trapezoid ABCD with median Prove: [Hint: X is the midpoint of auxiliary diagonal .]](https://storage.examlex.com/TB7237/11eb4b36_770b_04b5_a05a_59dc4a48d610_TB7237_11.jpg) -Use the drawing shown to explain the following theorem.
"The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases."
Given: Trapezoid ABCD with median
-Use the drawing shown to explain the following theorem.
"The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases."
Given: Trapezoid ABCD with median ![-Use the drawing shown to explain the following theorem. The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases. Given: Trapezoid ABCD with median Prove: [Hint: X is the midpoint of auxiliary diagonal .]](https://storage.examlex.com/TB7237/11eb4b36_770b_04b6_a05a_8b919b6290ac_TB7237_11.jpg) Prove:
Prove: ![-Use the drawing shown to explain the following theorem. The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases. Given: Trapezoid ABCD with median Prove: [Hint: X is the midpoint of auxiliary diagonal .]](https://storage.examlex.com/TB7237/11eb4b36_770b_04b7_a05a_d9b26ae03aaf_TB7237_11.jpg) [Hint: X is the midpoint of auxiliary diagonal
[Hint: X is the midpoint of auxiliary diagonal ![-Use the drawing shown to explain the following theorem. The length of the median of a trapezoid equals one-half the sum of the lengths of the two bases. Given: Trapezoid ABCD with median Prove: [Hint: X is the midpoint of auxiliary diagonal .]](https://storage.examlex.com/TB7237/11eb4b36_770b_04b8_a05a_3bcb21128df7_TB7237_11.jpg) .]
.]
(Essay)
4.9/5  (33)
(33)
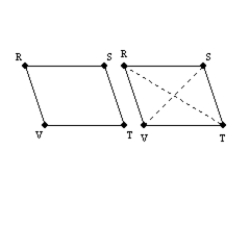 -Consider the drawing provided. Using the auxiliary diagonals (shown dashed), explain why the "opposite angles and opposite sides of a parallelogram must be congruent."
-Consider the drawing provided. Using the auxiliary diagonals (shown dashed), explain why the "opposite angles and opposite sides of a parallelogram must be congruent."
(Essay)
4.8/5  (36)
(36)
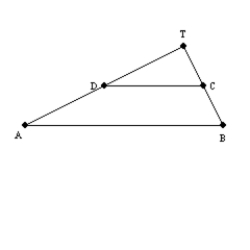 -Supply all statements and all reasons for the following proof.
Given:
-Supply all statements and all reasons for the following proof.
Given: 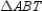 ; M is the midpoint of
; M is the midpoint of 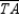 and N is the midpoint of
and N is the midpoint of 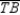 Prove: MNAB is a trapezoid
Prove: MNAB is a trapezoid
(Essay)
4.8/5  (37)
(37)
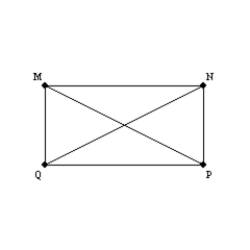 -Supply missing statements and missing reasons for the following proof.
Given: Rectangle MNPQ with diagonals
-Supply missing statements and missing reasons for the following proof.
Given: Rectangle MNPQ with diagonals 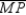 and
and 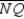 Prove:
Prove: 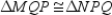 S1. R1.
S2.
S1. R1.
S2. 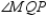 and
and  are rt.
are rt.  R2.
S3.
R2.
S3.  R3.
S4. R4. The diagonals of a rectangle are congruent.
S5. R5.
R3.
S4. R4. The diagonals of a rectangle are congruent.
S5. R5.
(Essay)
4.9/5  (36)
(36)
 -Provide the missing statements abd nissing reasons for the proof of this theorem.
"If both pairs of opposite sides of a quadrilateral are congruent, the quadrilateral is a parallelogram."
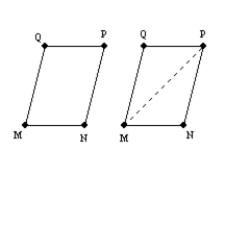
Given: Quad. MNPQ;
-Provide the missing statements abd nissing reasons for the proof of this theorem.
"If both pairs of opposite sides of a quadrilateral are congruent, the quadrilateral is a parallelogram."
Given: Quad. MNPQ;  and
and 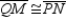 Prove: MNPQ is a parallelogram
S1. R1. Given
S2. Draw diagonal
Prove: MNPQ is a parallelogram
S1. R1. Given
S2. Draw diagonal 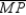 R2.
S3. R3. Identity
S4. R4. SSS
S5.
R2.
S3. R3. Identity
S4. R4. SSS
S5. 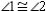 R5.
S6. R6. If 2 lines are cut by a trans. so that alternate interior angles
are congruent, these lines are parallel.
S7.
R5.
S6. R6. If 2 lines are cut by a trans. so that alternate interior angles
are congruent, these lines are parallel.
S7. 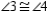 R7.
S8.
R7.
S8. 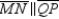 R8.
S9. R9.
R8.
S9. R9.
(Essay)
4.9/5  (37)
(37)
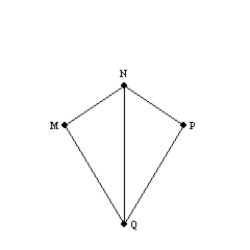 -Supply missing statements and missing reasons for this proof.
Given: Kite MNPQ with diagonal
-Supply missing statements and missing reasons for this proof.
Given: Kite MNPQ with diagonal 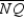 ;
;  and
and 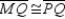 Prove:
Prove: 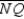 bisects
bisects 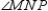 S1. R1.
S2.
S1. R1.
S2. 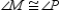 R2. In a kite, one pair of opposite angles are congruent.
S3.
R2. In a kite, one pair of opposite angles are congruent.
S3. 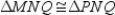 R3.
S4.
R3.
S4. 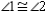 R4.
S5. R5.
R4.
S5. R5.
(Essay)
4.9/5  (41)
(41)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)