Exam 9: Surfaces and Solids
![-Use the drawing to explain the following theorem. The lateral area L of a regular pyramid with slant height of length l and perimeter P for the base is given by . [Note: Except for the number of sides for the base, the proof (argument) will not change for another regular polygon.] Given: Regular polygon with slant height of length l and length s for each side of the base Prove:](https://storage.examlex.com/TB7237/11eb4b36_76f5_a839_a05a_31200ff1c7ee_TB7237_11.jpg) -Use the drawing to explain the following theorem.
"The lateral area L of a regular pyramid with slant height of length l and perimeter P for the base is given by
-Use the drawing to explain the following theorem.
"The lateral area L of a regular pyramid with slant height of length l and perimeter P for the base is given by ![-Use the drawing to explain the following theorem. The lateral area L of a regular pyramid with slant height of length l and perimeter P for the base is given by . [Note: Except for the number of sides for the base, the proof (argument) will not change for another regular polygon.] Given: Regular polygon with slant height of length l and length s for each side of the base Prove:](https://storage.examlex.com/TB7237/11eb4b36_76f5_a83a_a05a_29378e2f1c46_TB7237_11.jpg) ."
[Note: Except for the number of sides for the base, the proof (argument) will not change
for another regular polygon.]
Given: Regular polygon with slant height of length l
and length s for each side of the base
Prove:
."
[Note: Except for the number of sides for the base, the proof (argument) will not change
for another regular polygon.]
Given: Regular polygon with slant height of length l
and length s for each side of the base
Prove: ![-Use the drawing to explain the following theorem. The lateral area L of a regular pyramid with slant height of length l and perimeter P for the base is given by . [Note: Except for the number of sides for the base, the proof (argument) will not change for another regular polygon.] Given: Regular polygon with slant height of length l and length s for each side of the base Prove:](https://storage.examlex.com/TB7237/11eb4b36_76f5_cf4b_a05a_b52e05881014_TB7237_11.jpg)
The faces of the regular polygon are congruent triangles. For each face, the altitude has
length l while the corresponding base length is s. Thus, the area of each of the n faces is 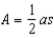 . The lateral area L is the sum of areas of all lateral faces. That is,
. The lateral area L is the sum of areas of all lateral faces. That is, 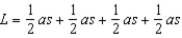 ,
, 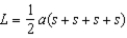 Because
Because 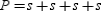 , the formula for the lateral area becomes
, the formula for the lateral area becomes 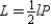 .
.
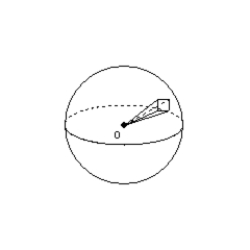 -Knowing that the surface area of a sphere is given by
-Knowing that the surface area of a sphere is given by 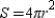 , complete the proof of the
volume formula for the sphere. Having separated the sphere into n pyramids ( each with the center of the sphere for its vertex), show that the volume of the sphere is
, complete the proof of the
volume formula for the sphere. Having separated the sphere into n pyramids ( each with the center of the sphere for its vertex), show that the volume of the sphere is 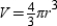 .
.
The volume of the sphere is the approximation of the sum of the volumes of the n pyramids.
Where the areas of the bases are 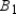 ,
, 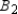 ,
, 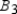 , and so on through
, and so on through 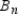 , the corresponding altitudes all have a length approximated by h. The the volume of the sphere is appproximated by
, the corresponding altitudes all have a length approximated by h. The the volume of the sphere is appproximated by 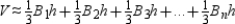 . In turn,
. In turn, 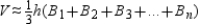 .
.
As n increases, the length h of the altitudes of the pyramids approaches r, the length of the radius of the sphere; that is, 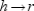 . As n increases, the combined base areas of the pyramids also approaches the surface area S of the sphere; that is,
. As n increases, the combined base areas of the pyramids also approaches the surface area S of the sphere; that is, 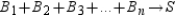 .
.
As n increases, we find that 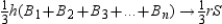 or
or 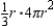 , so that
, so that 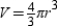 .
.
For a right circular cone, the length of the radius of the base is r, the length of the slant height
is l, and the length of the altitude is h. Given the lengths for r and h, explain why the length
of the slant height is given by 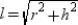 . (no drawing provided)
. (no drawing provided)
The radius, slant height from the vertex of the cone to the endpoint of the radius, and the altitude form a right triangle with l for the length of the hypotenuse. Then, 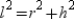 .
.
By the Square Roots Property, 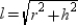 .
.
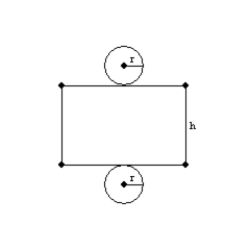 -Use the drawing to explain the following theorem.
"The total area of a right circular cylinder with base area B and lateral area L is given by
-Use the drawing to explain the following theorem.
"The total area of a right circular cylinder with base area B and lateral area L is given by 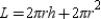 ."
."
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)