Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests

Which of the following would be an appropriate alternative hypothesis?

Suppose, in testing a hypothesis about a mean, the p-value is computed to be 0.034. The null hypothesis should be rejected if the chosen level of significance is 0.01.

TABLE 9-1 Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is greater than 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases: 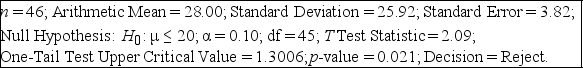-Referring to Table 9-1, what critical value should the manager use to determine the rejection region?

TABLE 9-4 A drug company is considering marketing a new local anesthetic. The effective time of the anesthetic the drug company is currently producing has a normal distribution with an mean of 7.4 minutes with a standard deviation of 1.2 minutes. The chemistry of the new anesthetic is such that the effective time should be normally distributed with the same standard deviation, but the mean effective time may be lower. If it is lower, the drug company will market the new anesthetic; otherwise, they will continue to produce the older one. A sample of size 36 results in a sample mean of 7.1. A hypothesis test will be done to help make the decision. -Referring to Table 9-4, the p-value of the test is ________.

A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. State the test of hypothesis that is of interest to the rental chain.

TABLE 9-6 The quality control engineer for a furniture manufacturer is interested in the mean amount of force necessary to produce cracks in stressed oak furniture. She performs a two-tail test of the null hypothesis that the mean for the stressed oak furniture is 650. The calculated value of the Z test statistic is a positive number that leads to a p-value of 0.080 for the test. -Referring to Table 9-6, suppose the engineer had decided that the alternative hypothesis to test was that the mean was greater than 650. Then if the test is performed with a level of significance of 0.05, the null hypothesis would be rejected.

TABLE 9-4 A drug company is considering marketing a new local anesthetic. The effective time of the anesthetic the drug company is currently producing has a normal distribution with an mean of 7.4 minutes with a standard deviation of 1.2 minutes. The chemistry of the new anesthetic is such that the effective time should be normally distributed with the same standard deviation, but the mean effective time may be lower. If it is lower, the drug company will market the new anesthetic; otherwise, they will continue to produce the older one. A sample of size 36 results in a sample mean of 7.1. A hypothesis test will be done to help make the decision. -Referring to Table 9-4, if the level of significance had been chosen as 0.05, the null hypothesis would be rejected.

TABLE 9-1 Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is greater than 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases: 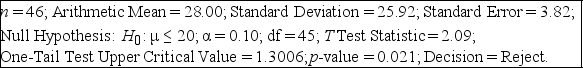-Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is greater than 20 during the morning shift using a level of significance of 0.10.

TABLE 9-1 Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is greater than 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases: 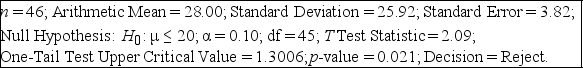-Referring to Table 9-1, the lowest level of significance at which the null hypothesis can be rejected is ________.

The test statistic measures how close the computed sample statistic has come to the hypothesized population parameter.

For a given sample size n, if the level of significance (α) is decreased, the power of the test

The statement of the null hypothesis always contains an equality.

The power of a test is measured by its capability of

If the Type I error (α) for a given test is to be decreased, then for a fixed sample size n

TABLE 9-7 A major home improvement store conducted its biggest brand recognition campaign in the company's history. A series of new television advertisements featuring well-known entertainers and sports figures was launched. A key metric for the success of television advertisements is the proportion of viewers who "like the ads a lot." A study of 1,189 adults who viewed the ads reported that 230 indicated that they "like the ads a lot." The percentage of a typical television advertisement receiving the "like the ads a lot" score is believed to be 22%. Company officials wanted to know if there is evidence that the series of television advertisements are less successful than the typical ad (i.e. if there is evidence that the population proportion of "like the ads a lot" for the company's ads is less than 0.22) at a 0.01 level of significance. -Referring to Table 9-7, state the alternative hypothesis for this study.

You know that the level of significance (α) of a test is 5%, you can tell that the probability of committing a Type II error (β) is

The owner of a local nightclub has recently surveyed a random sample of n = 250 customers of the club. She would now like to determine whether or not the mean age of her customers is greater than 30. If so, she plans to alter the entertainment to appeal to an older crowd. If not, no entertainment changes will be made. The appropriate hypotheses to test are:

A sample is used to obtain a 95% confidence interval for the mean of a population. The confidence interval goes from 15 to 19. If the same sample had been used to test the null hypothesis that the mean of the population is equal to 20 versus the alternative hypothesis that the mean of the population differs from 20, the null hypothesis could be rejected at a level of significance of 0.10.

Which of the following would be an appropriate null hypothesis?

How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: X = 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following conclusion is correct?