Exam 1: Functions and Change
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Of the functions 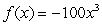 ,
, 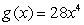 , and
, and  , which has the largest value as
, which has the largest value as 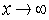 ?
?
(Multiple Choice)
5.0/5  (31)
(31)
Write in factored form the equation of the polynomial graphed below. All key features are shown. 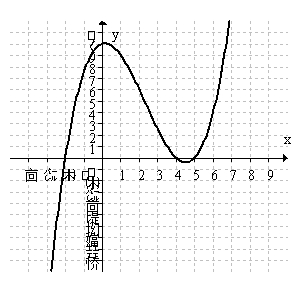
(Short Answer)
4.9/5  (38)
(38)
A town has 2400 people initially. Find the formula for the population of the town, P, in terms of the number of years, t, if the town grows by 70 people a year.
(Multiple Choice)
4.9/5  (45)
(45)
A bakery has 800 pounds of flour. If they use 5% of the available flour each day, how many pounds do they have left after 9 days? Round to the nearest pound.
(Short Answer)
4.9/5  (25)
(25)
In the following graph, the leading coefficient is ________(positive/negative) 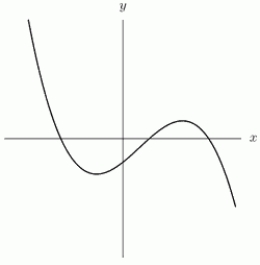
(Short Answer)
4.9/5  (31)
(31)
Give a possible formula for the function shown in the following table. 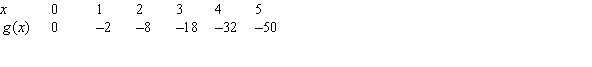
(Short Answer)
4.8/5  (20)
(20)
Write the Roman numeral of the graph that corresponds to each function.
A. 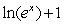 B.
B. 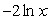 C.
C. 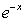 D.
D. 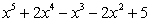
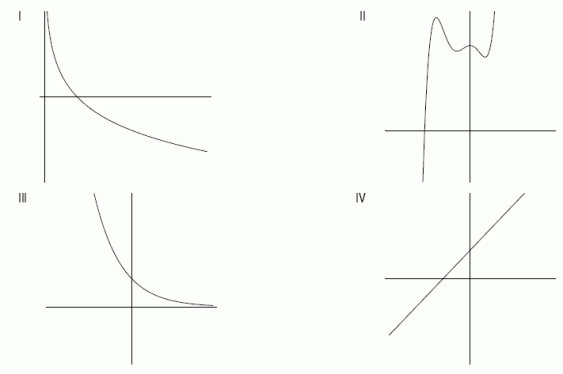
(Short Answer)
4.8/5  (28)
(28)
In nature, the populations of two animals, one of which preys upon the other (such as foxes and rabbits) are observed to oscillate with time, and are found to be well approximated by trigonometric functions. The population of foxes is shown in the graph below. Find the period. 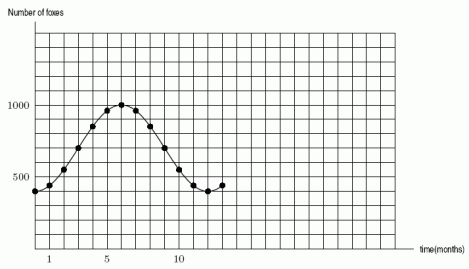
(Short Answer)
4.9/5  (32)
(32)
A population is growing according to the formula 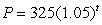 , where P is the population at year t. What is the annual growth rate?
, where P is the population at year t. What is the annual growth rate?
(Multiple Choice)
4.9/5  (34)
(34)
The following table shows values for an exponential function, 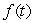 . Find a formula for
. Find a formula for 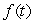 . Table entries are rounded to two decimal places.
. Table entries are rounded to two decimal places. 
(Short Answer)
4.8/5  (39)
(39)
A substance has a half-life of 56 years. What percent of the original amount of the substance will remain after 20 years? Round to the nearest percent.
(Short Answer)
4.9/5  (43)
(43)
Use shifts of power functions to find a possible formula for the following graph. 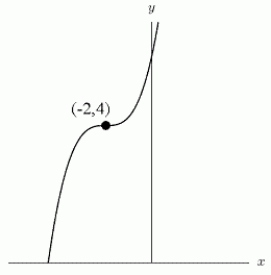
(Multiple Choice)
4.8/5  (38)
(38)
The following functions represent exponential growth or decay. Which ones represent continuous growth or decay? Select all that apply.
(Multiple Choice)
4.8/5  (42)
(42)
A population of rabbits is growing. In 2006, there were 10,000,000 rabbits, and the rate of increase was 10% per decade. Find 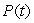 , the formula to predict the population t years after 2006.
, the formula to predict the population t years after 2006.
(Multiple Choice)
4.8/5  (27)
(27)
The cost of shipping r grams of material is given by the function 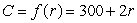 . Find a formula for the inverse function,
. Find a formula for the inverse function, 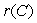 .
.
(Multiple Choice)
4.8/5  (41)
(41)
The population 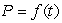 of the United States in millions t years after 1790 during the years from 1790 to 1860 was given approximately by the exponential formula
of the United States in millions t years after 1790 during the years from 1790 to 1860 was given approximately by the exponential formula 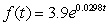 . What was the approximate doubling time for the population? Round to the nearest year.
. What was the approximate doubling time for the population? Round to the nearest year.
(Short Answer)
4.8/5  (31)
(31)
A town has 800 people initially. Find the formula for the population of the town, P, in terms of the number of years, t, if the town shrinks at an annual rate of 13% a year.
(Multiple Choice)
4.8/5  (36)
(36)
A new species, introduced into an environment in which it has no natural predators, grows exponentially with continuous growth rate k=0.095 per year. There are initially 45 individuals introduced. Write the formula for 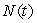 , the number of individuals after t years and use it to find how many years will it take for the population to reach 300 individuals. Round to 2 decimal places.
, the number of individuals after t years and use it to find how many years will it take for the population to reach 300 individuals. Round to 2 decimal places.
(Short Answer)
4.8/5  (34)
(34)
Showing 141 - 160 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)