Exam 9: Mathematical Modeling Using Differential Equations
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Which one(s) of the following are solutions to the differential equation 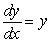 ?
?
Free
(Multiple Choice)
4.9/5  (47)
(47)
Correct Answer:
D
The amount of medicine present in the blood of a patient decreases due to metabolism according to the exponential decay model. One hour after a dose was given, there were 3.7 nanograms/cm3 present, and a hour later there were 2.5 ng/cm3. After how many hours will there be less than 0.8 ng/cm3 present, assuming no more medication is taken? Round to 1 decimal place.
Free
(Short Answer)
4.9/5  (40)
(40)
Correct Answer:
4.9
Mark all of the differential equations that are NOT separable.
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
A, B, C
A radioactive isotope decays at a continuous rate of approximately 15% per day. If A is the amount of the isotope and t is time in days, what is the differential equation for this situation and its general solution?
(Multiple Choice)
4.8/5  (30)
(30)
The fox eats the hare, so it needs it to survive. The hare would do fine without the fox. Which (if any) of the following systems of differential equations model the interaction between the fox and the hare, with the fox as x and the hare as y? Select all that apply.
(Multiple Choice)
4.9/5  (37)
(37)
A person withdraws money from a trust fund at a rate of $12,000 per year, and the account is earning interest at a rate of 5% per year, compounded continuously. Write a differential equation for the balance, B, in the account as a function of time, t, in years and use it to calculate 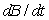 if B=$100,000.
if B=$100,000.
(Short Answer)
4.9/5  (35)
(35)
A person receives a drug intravenously at the rate of 3 mg per hour. The drug is eliminated from the body at a rate proportional to the amount present with a constant of proportionality of k = -0.4. What is the long term amount of the drug in the body, once the system has stabilized?
(Short Answer)
4.8/5  (38)
(38)
The equilibrium solution for 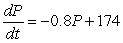 is P = _____. This solution is ________ (stable/unstable).
is P = _____. This solution is ________ (stable/unstable).
(Short Answer)
5.0/5  (30)
(30)
A quantity Q satisfies the differential equation 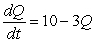 . Is Q increasing or decreasing at Q = 3?
. Is Q increasing or decreasing at Q = 3?
(Short Answer)
4.7/5  (40)
(40)
According to Newton, the rate at which the temperature of water in a swimming pool changes is directly proportional to the difference between the temperature L outside and the temperature T of the water in the pool. Suppose the temperature outside stays at a constant 28 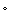 C for two hours, and that during that time the temperature of the water increases from 20
C for two hours, and that during that time the temperature of the water increases from 20 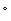 C to 24
C to 24 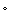 C. Which of the following shows the differential equation for this situation and its solution?
C. Which of the following shows the differential equation for this situation and its solution?
(Multiple Choice)
4.8/5  (33)
(33)
For S and I satisfying the differential equations 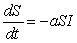
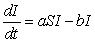 ,
is I increasing or decreasing when
,
is I increasing or decreasing when 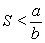 ?
?
(Short Answer)
5.0/5  (31)
(31)
Given that 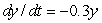 and that
and that 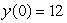 , estimate
, estimate 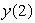 to 2 decimal places by first estimating y(1). Assume that the rate of growth given by
to 2 decimal places by first estimating y(1). Assume that the rate of growth given by 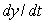 is approximately constant over each unit time interval.
is approximately constant over each unit time interval.
(Short Answer)
4.8/5  (37)
(37)
A lake with constant volume V, in km3, contains a quantity of Q km3 pollutant. Clean water enters the lake and causes a total outflow of r km3 per year. The rate at which the pollutant decreases at any time t equals the product of the pollutant Q per volume V and the rate at which the water flows out of the lake. If 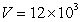 km3 and
km3 and 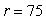 km3 per year, how many years will it take for the pollutant to decrease to half of its original quantity? Round to the nearest whole year.
km3 per year, how many years will it take for the pollutant to decrease to half of its original quantity? Round to the nearest whole year.
(Short Answer)
5.0/5  (43)
(43)
According to Newton, the rate at which the temperature of water in a swimming pool changes is directly proportional to the difference between the temperature L outside and the temperature T of the water in the pool. Suppose the temperature outside stays at a constant 28 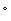 C for two hours, and that during that time the temperature of the water increases from 20
C for two hours, and that during that time the temperature of the water increases from 20 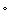 C to 24
C to 24 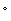 C. What is the equilibrium solution to the equation modeling this situation?
C. What is the equilibrium solution to the equation modeling this situation?
(Short Answer)
4.8/5  (38)
(38)
Carbon-14 decays at a rate proportional to the amount present. Which of the following is the differential equation for the amount, C, of carbon-14 present at time t?
(Multiple Choice)
4.7/5  (29)
(29)
If no more pollutants are dumped into a lake, the amount of pollution in the lake will decrease at a rate proportional to the amount of pollution present. If there are 400 units of pollution present initially and 184 units left after 8 years, use differential equations to find the number of units left after 13 years. Round to 1 decimal place.
(Short Answer)
4.9/5  (40)
(40)
On January 1, 1879, records show that 500 of a fish called Atlantic striped bass were introduced into the San Francisco Bay. In 1899, the first year fishing for bass was allowed, 100,000 of these bass were caught, representing 10% of the population at the start of 1899. Owing to reproduction, at any time the bass population is growing at a rate proportional to the population at that moment. Assume that when fishing starts in 1899, the rate at which bass are caught is proportional to the square of the population with constant of proportionality 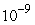 . What happens to the bass population in the long run?
. What happens to the bass population in the long run?
(Multiple Choice)
4.8/5  (35)
(35)
What is the solution to the differential equation 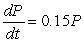 , given that P = 5 when t = 0?
, given that P = 5 when t = 0?
(Short Answer)
4.8/5  (27)
(27)
Consider the differential equation for the logistic model representing a population of tarantulas introduced into a new habitat: 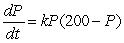 . What is the carrying capacity?
. What is the carrying capacity?
(Multiple Choice)
4.9/5  (25)
(25)
For 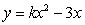 to be a solution to the differential equation
to be a solution to the differential equation 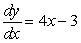 , what must be the constant k?
, what must be the constant k?
(Multiple Choice)
4.8/5  (34)
(34)
Showing 1 - 20 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)