Exam 8: Interval Estimates for Proportions, Mean Differences and Proportion Differences
Exam 1: An Introduction to Statistics44 Questions
Exam 2: Descriptive Statistics I: Elementary Data Presentation and Description147 Questions
Exam 3: Descriptive Statistics II: Additional Descriptive Measures and Data Displays128 Questions
Exam 4: Probability147 Questions
Exam 5: Discrete Probability Distributions144 Questions
Exam 6: Continuous Probability Distributions141 Questions
Exam 7: Statistical Inference: Estimating a Population Mean134 Questions
Exam 8: Interval Estimates for Proportions, Mean Differences and Proportion Differences19 Questions
Exam 9: Statistical Hypothesis Testing: Hypothesis Tests for a Population Mean62 Questions
Exam 10: Hypothesis Tests for Proportions, Mean Differences and Proportion Differences39 Questions
Exam 11: Basic Regression Analysis111 Questions
Exam 12: Multiple Regression53 Questions
Exam 13: F Tests and Analysis of Variance95 Questions
Exam 14: Experimental Designonline Only64 Questions
Exam 16: Chi-Square Tests145 Questions
Select questions type
In a matched sample design, one uses the average for each pair of data values when building a confidence interval.
Free
(True/False)
4.8/5  (37)
(37)
Correct Answer:
False
In a 95% confidence interval estimate of the difference between two population means, the standard error of the proportion will be 1.96 times the margin of error.
Free
(True/False)
4.9/5  (35)
(35)
Correct Answer:
False
For large enough sample sizes, 95% of the possible sample mean differences will be within 1.96 standard errors of the population mean difference.
Free
(True/False)
5.0/5  (43)
(43)
Correct Answer:
True
When calculating the sample size to use in estimating a population proportion, using a proportion equal to 0.25 will provide the maximum sample size.
(True/False)
4.8/5  (35)
(35)
When each data value in one sample is paired with a corresponding data value in another sample, the samples are said to be independent.
(True/False)
4.8/5  (45)
(45)
For the sampling distribution of the sample proportion, the distribution is approximately normal as long as n < 30.
(True/False)
4.9/5  (32)
(32)
One of the properties of the sampling distribution of the sample proportion is that the expected value of the sample proportion will be exactly equal to 0.5.
(True/False)
4.8/5  (42)
(42)
In the absence of any other information, determining the largest sample size that might be necessary to build a 95% confidence interval estimate of a population proportion requires us to assume that the population proportion is .50.
(True/False)
4.8/5  (43)
(43)
A 95% confidence interval estimate of the difference between two population proportions will contain 95% of the possible sample proportion differences.
(True/False)
4.9/5  (33)
(33)
In a 95% confidence interval estimate of a population proportion, the margin of error will be 2.33 times the standard error of the proportion.
(True/False)
4.8/5  (30)
(30)
As the sample size increases, the margin of error in an interval estimate of a population proportion decreases.
(True/False)
4.9/5  (35)
(35)
In any confidence interval estimate of a population proportion difference, the margin of error will be less than the standard error of the sampling distribution.
(True/False)
4.8/5  (34)
(34)
A matched sample design can lead to a smaller sampling error than the independent sample design because some or all of the variation between sampled items is eliminated as a source of sampling error.
(True/False)
4.8/5  (38)
(38)
An interval estimate of a population proportion is a range of values used to estimate the population parameter .
(True/False)
5.0/5  (37)
(37)
As the confidence requirement increases, the standard error term in an interval estimate of the difference between two population proportions decreases.
(True/False)
4.9/5  (37)
(37)
The sampling distribution of the sample proportion is the probability distribution of all possible values of the sample proportion when a sample of size n is taken from a particular population.
(True/False)
4.9/5  (36)
(36)
The sampling distribution of the sample mean difference is the probability distribution of all possible values of the sample mean difference when a sample of size n1 is taken from one population and a sample of size n2 is taken from another.
(True/False)
4.8/5  (38)
(38)
In determining a confidence interval for the difference between two population proportions, the point estimate of the difference is ( 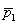 -
- 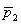 ).
).
(True/False)
4.8/5  (25)
(25)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)