Exam 9: Infinite Series
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Consider the function given by 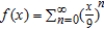 . Find the interval of convergence for
. Find the interval of convergence for 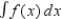 .
.
(Multiple Choice)
4.8/5  (32)
(32)
What is 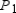 a first-degree polynomial function whose value and slope agree with the value and slope of
a first-degree polynomial function whose value and slope agree with the value and slope of 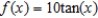 at
at 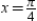 ?
?
(Multiple Choice)
4.8/5  (35)
(35)
Use the Root Test to determine the convergence or divergence of the series. 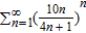
(Multiple Choice)
4.7/5  (43)
(43)
Write the first five terms of the sequence of partial sums. 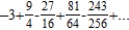
(Multiple Choice)
4.8/5  (29)
(29)
Use the Ratio Test to determine the convergence or divergence of the series. 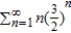
(Multiple Choice)
4.7/5  (37)
(37)
Use the Root Test to determine the convergence or divergence of the series 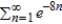 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Use the definition to find the Taylor series centered at 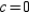 for the function
for the function 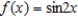 .
.
(Multiple Choice)
5.0/5  (29)
(29)
Determine the convergence or divergence of the series using any appropriate test from this chapter. Identify the test used. 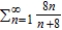
(Multiple Choice)
4.9/5  (29)
(29)
Find the fourth degree Maclaurin polynomial for the function. 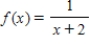
(Multiple Choice)
4.9/5  (33)
(33)
Approximate the sum of the series by using the first six terms. 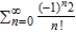
(Multiple Choice)
4.9/5  (35)
(35)
Find the sum of the convergent series 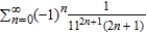 by using a well-known function. Round your answer to four decimal places.
by using a well-known function. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Determine the degree of the Maclaurin polynomial required for the error in the approximation of the function 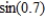 to be less than 0.001.
to be less than 0.001.
(Multiple Choice)
4.8/5  (30)
(30)
Determine the minimal number of terms required to approximate the sum of the series with an error of less than 0.001. 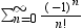
(Multiple Choice)
4.8/5  (42)
(42)
Use the polynomial test to determine whether the series 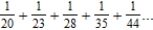 converges or diverges.
converges or diverges.
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the series 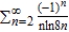 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
(Multiple Choice)
4.8/5  (38)
(38)
Use the Direct Comparison Test to determine the convergence or divergence of the series 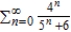 .
.
(Multiple Choice)
4.9/5  (43)
(43)
Showing 21 - 40 of 181
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)