Exam 8: Integration Techniques and Improper Integrals
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find the smallest n such that the error estimate in the approximation of the definite integral 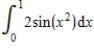 is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.
is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the improper integral 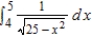 diverges or converges. Evaluate the integral if it converges.
diverges or converges. Evaluate the integral if it converges.
(Multiple Choice)
4.7/5  (33)
(33)
Determine whether the improper integral 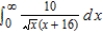 diverges or converges. Evaluate the integral if it converges.
diverges or converges. Evaluate the integral if it converges.
(Multiple Choice)
4.9/5  (37)
(37)
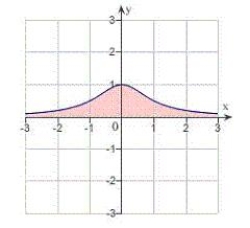
Find the area between the x-axis and the graph of the function 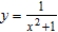 .
. 
(Multiple Choice)
4.8/5  (35)
(35)
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using 20 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 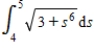
(Multiple Choice)
4.7/5  (37)
(37)
Find the smallest n such that the error estimate in the approximation of the definite integral 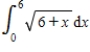 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.
(Multiple Choice)
4.8/5  (25)
(25)
Find the smallest n such that the error estimate in the approximation of the definite integral 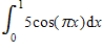 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.
(Multiple Choice)
4.8/5  (37)
(37)
A hydraulic cylinder on an industrial machine pushes a steel block a distance of x feet 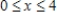 where the variable force required is
where the variable force required is 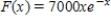 pounds. Find the work done in pushing the block the full 4 feet through the machine. Round your answer to three decimal places.
pounds. Find the work done in pushing the block the full 4 feet through the machine. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Use the error formula to estimate the error in approximating the integral 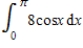 with
with 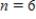 using Simpson's Rule. Round your answer to six decimal places.
using Simpson's Rule. Round your answer to six decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Determine whether the improper integral  diverges or converges.
diverges or converges.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 21 - 40 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)