Exam 15: Vector Anal
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
A tractor engine has a steel component with a circular base modeled by the vector-valued function  . Its height is given by
. Its height is given by 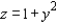 . (All measurements of the component are given in centimeters.) Find the lateral surface area of the component. Round your answer to two decimal places.
. (All measurements of the component are given in centimeters.) Find the lateral surface area of the component. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (32)
(32)
Identify the surface by eliminating the parameters from the vector-valued function 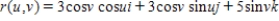 .
.
(Multiple Choice)
4.9/5  (36)
(36)
Evaluate 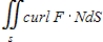 , where
, where 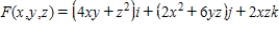 and S is the closed surface of the solid bounded by the graphs,
and S is the closed surface of the solid bounded by the graphs, 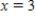 and
and 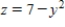 , and the coordinate planes.
, and the coordinate planes.
(Multiple Choice)
4.9/5  (26)
(26)
Let 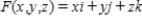 and let S be the cube bounded by the planes
and let S be the cube bounded by the planes 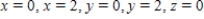 and
and 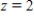 . Verify the Divergence Theorem by evaluating
. Verify the Divergence Theorem by evaluating 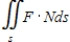 as a surface integral and as a triple integral.
as a surface integral and as a triple integral.
(Multiple Choice)
4.8/5  (32)
(32)
Find an equation of the tangent plane to the surface represented by the vector-valued function at the given point. 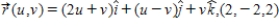
(Multiple Choice)
4.9/5  (38)
(38)
Set up and evaluate a line integral to find the area of the region R bounded by the graph of 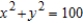 .
.
(Multiple Choice)
4.9/5  (44)
(44)
Determine whether or not the vector field is conservative. 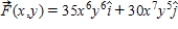
(Multiple Choice)
4.8/5  (33)
(33)
Determine whether the vector field is conservative. If it is, find a potential function for the vector field. 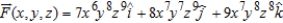
(Multiple Choice)
4.8/5  (30)
(30)
Find the maximum value of 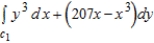 where
where 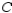 is any closed curve in the xy-plane, oriented counterclockwise.
is any closed curve in the xy-plane, oriented counterclockwise.
(Multiple Choice)
4.8/5  (31)
(31)
Find the work done by a person weighing 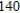 pounds walking exactly one revolution up a circular helical staircase of radius
pounds walking exactly one revolution up a circular helical staircase of radius 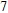 feet if the person rises
feet if the person rises 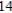 feet.
feet.
(Multiple Choice)
4.8/5  (46)
(46)
Use Stokes's Theorem to evaluate 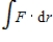 where
where 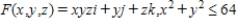 and S is the first-octant portion of
and S is the first-octant portion of 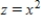 over
over 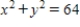 . Use a computer algebra system to verify your result.
. Use a computer algebra system to verify your result.
(Multiple Choice)
4.7/5  (38)
(38)
Evaluate 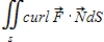 where S is the closed surface of the solid bounded by the graphs of
where S is the closed surface of the solid bounded by the graphs of 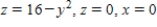 and
and 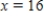 .
. 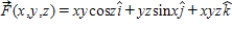
(Multiple Choice)
4.8/5  (34)
(34)
Find a piecewise smooth parametrization of the path C given in the following graph. 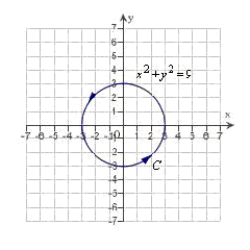
(Multiple Choice)
4.9/5  (34)
(34)
Let 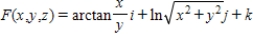 and let C be the triangle with vertices of
and let C be the triangle with vertices of 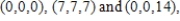 oriented counterclockwise. Use Stokes's Theorem to evaluate
oriented counterclockwise. Use Stokes's Theorem to evaluate 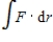 .
.
(Multiple Choice)
4.7/5  (30)
(30)
Find the flux  of through S,
of through S, 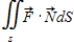 , where
, where 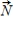 is the upward unit normal vector to S.
is the upward unit normal vector to S. 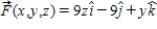
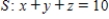 , first octant
, first octant
(Multiple Choice)
4.9/5  (43)
(43)
Evaluate the line integral using the Fundamental Theorem of Line Integrals. Use a computer algebra system to verify your results. 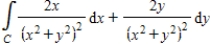
C: circle
C: circle 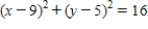 clockwise from
clockwise from 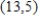 to
to 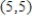
(Multiple Choice)
4.8/5  (46)
(46)
Showing 21 - 40 of 142
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)