Exam 15: Vector Anal
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Evaluate 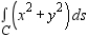 along the path C, defined as counterclockwise along the circle
along the path C, defined as counterclockwise along the circle 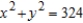 from
from 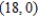 to
to 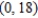 .
.
(Multiple Choice)
5.0/5  (43)
(43)
Use Green's Theorem to evaluate the integral 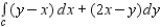 where
where 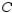 is the boundary of the region lying inside the rectangle bounded by
is the boundary of the region lying inside the rectangle bounded by 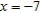 ,
, 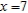 ,
,  ,
, 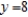 and outside the square bounded by
and outside the square bounded by 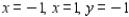 , and
, and 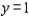 .
.
(Multiple Choice)
4.9/5  (43)
(43)
Let 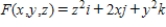 and let S be the graph of
and let S be the graph of 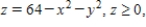 oriented counterclockwise. Use Stokes's Theorem to evaluate
oriented counterclockwise. Use Stokes's Theorem to evaluate 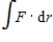 .
.
(Multiple Choice)
4.8/5  (28)
(28)
Find the gradient vector for the scalar function. (That is, find the conservative vector field for the potential function.) 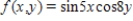
(Multiple Choice)
4.9/5  (33)
(33)
Find a piecewise smooth parametrization of the path C given in the following graph. 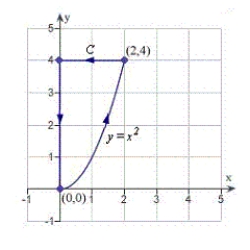
(Multiple Choice)
4.8/5  (35)
(35)
Calculate the line integral along 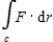 for
for 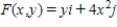 and C is any path starting at the point
and C is any path starting at the point 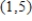 and ending at
and ending at 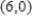 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Use the Divergence Theorem to evaluate 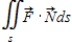 and find the outward flux of
and find the outward flux of  through the surface of the solid bounded by the graphs of the equations. Use a computer algebra system to verify your results.
through the surface of the solid bounded by the graphs of the equations. Use a computer algebra system to verify your results. 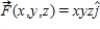
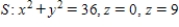
(Multiple Choice)
4.8/5  (43)
(43)
Find the area of the lateral surface over the curve 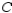 in the xy-plane and under the surface
in the xy-plane and under the surface 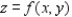 where Lateral surface
where Lateral surface 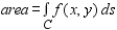 .
. 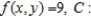 line from
line from 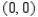 to
to 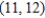 .
.
(Multiple Choice)
4.7/5  (38)
(38)
Use Green's Theorem to evaluate the integral 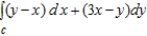
For the path C: boundary of the region lying between the graphs of
For the path C: boundary of the region lying between the graphs of 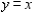 and
and 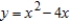 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Use a computer algebra system and the result "The centroid of the region having area A bounded by the simple closed path 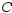 is
is 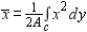 ,
, 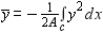 '' to find the centroid of the region bounded by the graphs of
'' to find the centroid of the region bounded by the graphs of 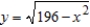 and
and 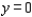 .
.
(Multiple Choice)
4.9/5  (37)
(37)
Use Divergence Theorem to evaluate 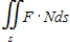 and find the outward flux of
and find the outward flux of 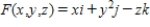 through the surface S of the solid bounded by
through the surface S of the solid bounded by 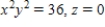 and
and 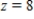 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Find the rectangular equation for the surface by eliminating the parameters from the vector-valued function 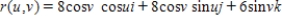 .
.
(Multiple Choice)
4.9/5  (37)
(37)
Find the divergence of the vector field at the given point. 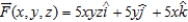 ,
, 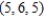
(Multiple Choice)
4.8/5  (33)
(33)
Find the rectangular equation for the surface by eliminating the parameters from the vector-valued function 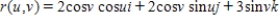 and sketch the graph.
and sketch the graph.
(Multiple Choice)
4.8/5  (50)
(50)
Showing 61 - 80 of 142
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)