Exam 12: Vector-Valued Functions
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find the point on the curve 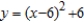 at which the curvature K is a maximum.
at which the curvature K is a maximum.
(Multiple Choice)
4.9/5  (39)
(39)
The smaller the curvature in a bend of a road, the faster a car can travel. Assume that the maximum speed around a turn is inversely proportional to the square root of the curvature. A car moving on the path 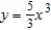 (x and y are measured in miles) can safely go 30 miles per hour at
(x and y are measured in miles) can safely go 30 miles per hour at 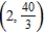 . How fast can it go at
. How fast can it go at 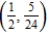 ? Round your answer to two decimal places.
? Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (37)
(37)
Use the given acceleration function and initial conditions to find the position at time t = 4. 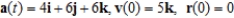
(Multiple Choice)
4.9/5  (33)
(33)
Sketch the curve represented by the vector-valued function 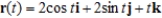 and give the orientation of the curve.
and give the orientation of the curve.
(Multiple Choice)
4.9/5  (39)
(39)
The quarterback of a football team releases a pass at a height of 6 feet above the playing field, and the football is caught by a receiver 62 yards directly downfield at a height of 3 feet. The pass is released at an angle of 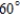 with the horizontal. Find the maximum height of the football. Round your answer to one decimal place.
with the horizontal. Find the maximum height of the football. Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (39)
(39)
Determine the interval on which the vector-valued function 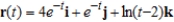 is continuous.
is continuous.
(Multiple Choice)
5.0/5  (36)
(36)
Find the arc length for 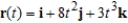 over the interval
over the interval 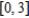 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (41)
(41)
Use the properties of the derivative to find 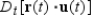 given the following vector-valued functions.
given the following vector-valued functions. 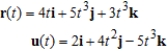
(Multiple Choice)
4.8/5  (37)
(37)
Suppose the two particles travel along the space curves 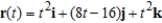 and
and 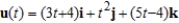 . A collision will occur at the point of intersection P if both particles are at P at the same time. Find the point of collision.
. A collision will occur at the point of intersection P if both particles are at P at the same time. Find the point of collision.
(Multiple Choice)
4.9/5  (40)
(40)
The graph below is most likely the graph of which of the following equations? 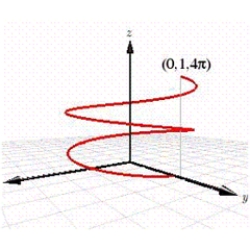
(Multiple Choice)
4.9/5  (43)
(43)
Use the properties of the derivative to find 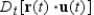 given the following vector-valued functions.
given the following vector-valued functions. 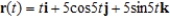
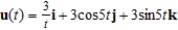
(Multiple Choice)
4.8/5  (37)
(37)
The position vector 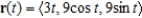 describes the path of an object moving in space. Find the speed
describes the path of an object moving in space. Find the speed 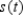 of the object.
of the object.
(Multiple Choice)
4.7/5  (36)
(36)
A baseball, hit 7 feet above the ground, leaves the bat at an angle of 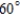 and its caught by an outfielder 7 feet above the ground and 400 feet from home plate. How high does the ball rise? Round your answer to the nearest integer.
and its caught by an outfielder 7 feet above the ground and 400 feet from home plate. How high does the ball rise? Round your answer to the nearest integer.
(Multiple Choice)
4.9/5  (35)
(35)
Determine the range of a projectile fired at a height of 3 feet above the ground with an initial velocity of 500 feet per second and at an angle of 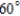 above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
(Multiple Choice)
4.7/5  (32)
(32)
Use the properties of the derivative to find 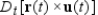 given the following vector-valued functions.
given the following vector-valued functions. 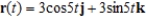
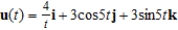
(Multiple Choice)
4.8/5  (37)
(37)
Use the given acceleration function and initial conditions to find the position at time t = 3. 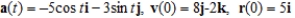
(Multiple Choice)
4.8/5  (36)
(36)
Showing 41 - 60 of 85
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)