Exam 13: Vector Calculus
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Let 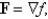 where
where 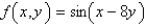 .Which of the following equations does the line segment from
.Which of the following equations does the line segment from 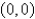 to
to 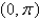 satisy?
satisy?
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
B
Let f be a scalar field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.curl f
Free
(Short Answer)
4.9/5  (36)
(36)
Correct Answer:
The curl is a property of vector fields, not scalar fields. So, curl f is not meaningful.
Find the moment of inertia about the z-axis of a thin funnel in the shape of a cone 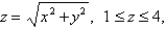 if its density function is
if its density function is 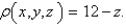
Free
(Short Answer)
4.8/5  (48)
(48)
Correct Answer:
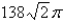
A particle is moving in a velocity field 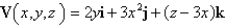 At time t = 1 the particle is located at the point (1, 5, 5).a). What is the velocity of the particle at t = 1?
b). What is the approximate location of the particle at t = 1.01?
At time t = 1 the particle is located at the point (1, 5, 5).a). What is the velocity of the particle at t = 1?
b). What is the approximate location of the particle at t = 1.01?
(Short Answer)
4.7/5  (30)
(30)
Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes 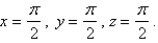
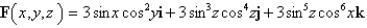
(Multiple Choice)
4.9/5  (34)
(34)
Use Stokes' Theorem to evaluate 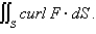
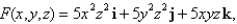
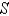 is the part of the paraboloid
is the part of the paraboloid 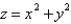 that lies inside the cylinder
that lies inside the cylinder 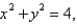 oriented upword.
oriented upword.
(Multiple Choice)
4.9/5  (36)
(36)
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. 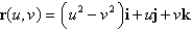 ;
; 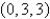
(Short Answer)
4.9/5  (36)
(36)
The temperature at the point 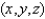 in a substance with conductivity
in a substance with conductivity 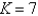 is
is 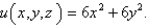 Find the rate of heat flow inward across the cylindrical
Find the rate of heat flow inward across the cylindrical 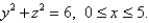
(Multiple Choice)
4.9/5  (33)
(33)
Find the work done by the force field 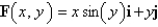 on a particle that moves along the parabola
on a particle that moves along the parabola 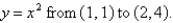
(Multiple Choice)
4.9/5  (40)
(40)
Use Stokes' Theorem to evaluate 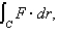 where
where 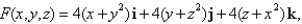 and
and 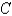 is the triangle with vertices
is the triangle with vertices 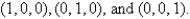
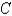 is oriented counterclockwise as viewed from above.
is oriented counterclockwise as viewed from above.
(Multiple Choice)
4.9/5  (24)
(24)
The flow lines (or streamlines) of a vector field are the paths followed by a particle whose velocity field is the given vector field. Thus, the vectors in a vector field are tangent to the flow lines. The flow lines of the vector field 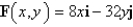 satisfy the differential equations
satisfy the differential equations 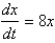 and
and 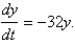 Solve these differential equations to find the equations of the family of flow lines.
Solve these differential equations to find the equations of the family of flow lines.
(Short Answer)
4.9/5  (33)
(33)
A particle starts at the point 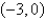 , moves along the x-axis to (3, 0) and then along the semicircle
, moves along the x-axis to (3, 0) and then along the semicircle 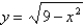 to the starting point. Use Green's Theorem to find the work done on this particle by the force field
to the starting point. Use Green's Theorem to find the work done on this particle by the force field 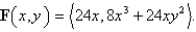
(Multiple Choice)
4.7/5  (30)
(30)
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 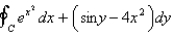 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 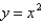 and
and 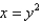 .
.
(Multiple Choice)
4.7/5  (32)
(32)
Evaluate the surface integral. 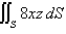 S is the part of the plane
S is the part of the plane 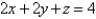 that lies in the first octant.
that lies in the first octant.
(Multiple Choice)
4.9/5  (37)
(37)
Use Gauss's Law to find the charge contained in the solid hemisphere 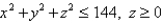 , if the electric field is
, if the electric field is 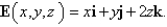
(Short Answer)
4.9/5  (30)
(30)
Use the Divergence Theorem to calculate the surface integral 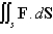 ; that is, calculate the flux of
; that is, calculate the flux of 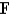 across
across 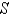 .
. 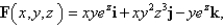 S is the surface of the box bounded by the coordinate planes and the planes
S is the surface of the box bounded by the coordinate planes and the planes 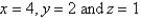 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Find the work done by the force field 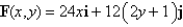 in moving an object along an arch of the cycloid
in moving an object along an arch of the cycloid 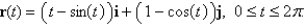
(Short Answer)
4.9/5  (30)
(30)
Evaluate the surface integral. Round your answer to four decimal places. 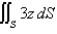 S is surface
S is surface 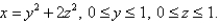
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)