Exam 13: Vector Calculus
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Determine whether or not vector field is conservative. If it is conservative, find a function f such that 

(Short Answer)
4.7/5  (32)
(32)
Use Stokes' Theorem to evaluate  where
where 
 is the curve of intersection of the plane
is the curve of intersection of the plane  and the cylinder
and the cylinder 
 is oriented counterclockwise as viewed from above.
is oriented counterclockwise as viewed from above.
(Multiple Choice)
4.7/5  (43)
(43)
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 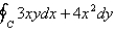 , where C is the triangle with vertices
, where C is the triangle with vertices  ,
,  , and
, and  .
.
(Multiple Choice)
4.8/5  (26)
(26)
Find (a) the divergence and (b) the curl of the vector field F. 
(Short Answer)
4.7/5  (29)
(29)
Find the area of the surface S where S is the part of the surface  that lies inside the cylinder
that lies inside the cylinder 
(Short Answer)
4.8/5  (33)
(33)
A plane lamina with constant density  occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are
occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are  Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and
Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and  .
.
(Multiple Choice)
4.9/5  (28)
(28)
Set up, but do not evaluate, a double integral for the area of the surface with parametric equations 
(Short Answer)
4.7/5  (26)
(26)
Evaluate the surface integral  for the given vector field F and the oriented surface S. In other words, find the flux of F across S.
for the given vector field F and the oriented surface S. In other words, find the flux of F across S. 

(Short Answer)
4.8/5  (27)
(27)
Suppose that F is an inverse square force field, that is,  where
where  Find the work done by F in moving an object from a point
Find the work done by F in moving an object from a point  along a path to a point
along a path to a point  in terms of the distances
in terms of the distances  and
and  from these points to the origin.
from these points to the origin.
(Short Answer)
4.9/5  (34)
(34)
Find the area of the surface S where S is the part of the plane  that lies above the triangular region with vertices
that lies above the triangular region with vertices 
 , and
, and 
(Short Answer)
4.7/5  (34)
(34)
Let D be a region bounded by a simple closed path C in the xy. Then the coordinates of the centroid  where A is the area of D.Find the centroid of the triangle with vertices (0, 0), (
where A is the area of D.Find the centroid of the triangle with vertices (0, 0), (  , 0) and (0,
, 0) and (0,  ).
).
(Multiple Choice)
4.9/5  (38)
(38)
Find a function f such that  , and use it to evaluate
, and use it to evaluate  along the given curve C.
along the given curve C. 

(Short Answer)
4.8/5  (32)
(32)
Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find  , where a is the constant vector.
, where a is the constant vector.
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether F is conservative. If so, find a function f such that  .
. 
(Multiple Choice)
4.9/5  (42)
(42)
A thin wire is bent into the shape of a semicircle  If the linear density is
If the linear density is  , find the exact mass of the wire.
, find the exact mass of the wire.
(Multiple Choice)
4.8/5  (31)
(31)
Use Green's Theorem to find the work done by the force  in moving a particle from the origin along the x-axis to (1, 0) then along the line segment to
(0, 1) and then back to the origin along the y-axis.
in moving a particle from the origin along the x-axis to (1, 0) then along the line segment to
(0, 1) and then back to the origin along the y-axis.
(Short Answer)
4.9/5  (32)
(32)
Showing 21 - 40 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)