Exam 12: Multiple Integrals
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Evaluate the iterated integral by converting to polar coordinates. Round the answer to two decimal places. 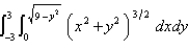 .
.
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
C
Find the volume under 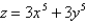 and above the region bounded by
and above the region bounded by 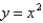 and
and 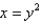 .
.
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
E
Use cylindrical or spherical coordinates, whichever seems more appropriate, to evaluate 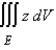 where E lies above the paraboloid
where E lies above the paraboloid 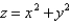 and below the plane
and below the plane 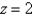 .
.
Free
(Multiple Choice)
4.7/5  (29)
(29)
Correct Answer:
E
Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices 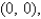
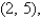 and
and 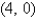 , and having the mass density
, and having the mass density 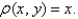
(Multiple Choice)
4.8/5  (32)
(32)
Sketch the solid whose volume is given by the iterated integral 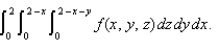
(Short Answer)
4.7/5  (34)
(34)
Evaluate the double integral by first identifying it as the volume of a solid. 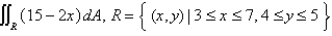
(Multiple Choice)
4.8/5  (29)
(29)
Use polar coordinates to find the volume of the solid bounded by the paraboloid 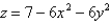 and the plane
and the plane 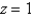 .
.
(Multiple Choice)
4.9/5  (40)
(40)
Evaluate the triple integral. Round your answer to one decimal place. 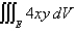
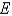 lies under the plane
lies under the plane 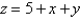 and above the region in the
and above the region in the 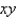 -plane bounded by the curves
-plane bounded by the curves 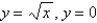 , and
, and 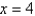 .
.
(Short Answer)
4.9/5  (30)
(30)
Express the volume of the wedge in the first octant that is cut from the cylinder 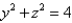 by the planes
by the planes 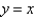 and
and 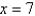 as an iterated integral with respect to
as an iterated integral with respect to 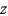 , then to
, then to 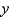 , then to
, then to 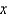 .
.
(Short Answer)
4.8/5  (32)
(32)
An electric charge is spread over a rectangular region 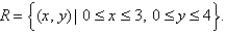 Find the total charge on R if the charge density at a point
Find the total charge on R if the charge density at a point 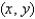 in R (measured in coulombs per square meter) is
in R (measured in coulombs per square meter) is 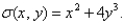
(Multiple Choice)
4.9/5  (34)
(34)
The double integral 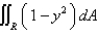 , where
, where 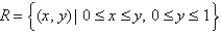 , gives the volume of a solid. Describe the solid.
, gives the volume of a solid. Describe the solid.
(Short Answer)
4.8/5  (31)
(31)
Evaluate the double integral 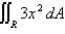 , where
, where 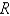 is the region bounded by the graphs of
is the region bounded by the graphs of 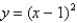 and
and 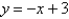 .
.
(Short Answer)
4.7/5  (32)
(32)
Find the mass of a solid hemisphere of radius 5 if the mass density at any point on the solid is directly proportional to its distance from the base of the solid.
(Multiple Choice)
5.0/5  (40)
(40)
A lamina occupies the part of the disk 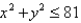 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
(Short Answer)
4.7/5  (23)
(23)
A cylindrical drill with radius 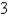 is used to bore a hole through the center of a sphere of radius
is used to bore a hole through the center of a sphere of radius 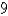 . Find the volume of the ring-shaped solid that remains. Round the answer to the nearest hundredth.
. Find the volume of the ring-shaped solid that remains. Round the answer to the nearest hundredth.
(Short Answer)
4.7/5  (27)
(27)
Find the center of mass of a homogeneous solid bounded by the paraboloid 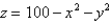 and
and 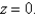
(Short Answer)
4.9/5  (31)
(31)
Evaluate the triple integral. Round your answer to one decimal place. 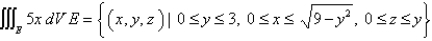
(Short Answer)
4.9/5  (39)
(39)
Calculate the double integral. Round your answer to two decimal places. 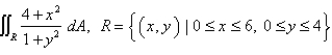
(Short Answer)
4.8/5  (37)
(37)
Showing 1 - 20 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)