Exam 4: Applications of Differentiation
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Sketch the graph of 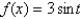 on
on 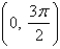 and find its absolute maximum and absolute minimum values, if any.
and find its absolute maximum and absolute minimum values, if any.
Free
(Short Answer)
4.9/5  (40)
(40)
Correct Answer:
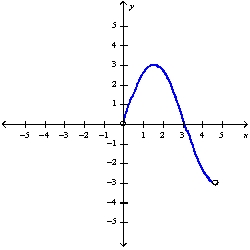 Abs. max.
Abs. max. 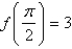
The sum of two positive numbers is 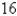 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
Free
(Short Answer)
4.8/5  (33)
(33)
Correct Answer:
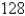
Find the critical number(s), if any of the function 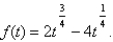
Free
(Multiple Choice)
4.7/5  (36)
(36)
Correct Answer:
A
A piece of wire 10 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (43)
(43)
Determine where the graph of 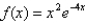 is concave upward and where it is concave downward. Also, find all inflection points of the function.
is concave upward and where it is concave downward. Also, find all inflection points of the function.
(Short Answer)
4.8/5  (37)
(37)
Use Newton's method with the specified initial approximation 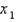 to find
to find 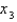 , the third approximation to the root of the given equation. (Give your answer to four decimal places.)
, the third approximation to the root of the given equation. (Give your answer to four decimal places.) 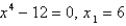
(Short Answer)
4.8/5  (42)
(42)
Use Newton's method with the specified initial approximation 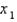 to find
to find 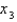 , the third approximation to the root of the given equation. (Round your answer to four decimal places.)
, the third approximation to the root of the given equation. (Round your answer to four decimal places.) 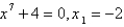
(Multiple Choice)
4.9/5  (43)
(43)
Find the absolute maximum and absolute minimum values, if any, of the function 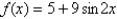 on
on 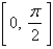 .
.
(Multiple Choice)
4.8/5  (36)
(36)
Find the position function of a particle moving along a coordinate line that satisfies the given condition. 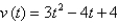 , s(1) = -1
, s(1) = -1
(Short Answer)
4.8/5  (43)
(43)
The graph of the derivative 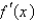 of a continuous function f is shown. On what intervals is f decreasing?
of a continuous function f is shown. On what intervals is f decreasing?  .
.
(Multiple Choice)
4.9/5  (38)
(38)
A car braked with a constant deceleration of 40  , producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
(Short Answer)
4.8/5  (45)
(45)
Find the number c that satisfies the conclusion of the Mean Value Theorem on the given interval. 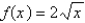 ,
, 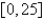
(Multiple Choice)
4.7/5  (38)
(38)
The function 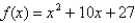 satisfies the hypotheses of Rolle's Theorem on the interval
satisfies the hypotheses of Rolle's Theorem on the interval 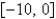 . Find all values of c that satisfy the conclusion of the theorem.
. Find all values of c that satisfy the conclusion of the theorem.
(Multiple Choice)
4.8/5  (43)
(43)
A woman at a point A on the shore of a circular lake with radius 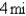 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of 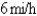 and row a boat at
and row a boat at 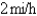 . How should she proceed? (Find
. How should she proceed? (Find 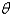 ). Round the result, if necessary, to the nearest hundredth.
). Round the result, if necessary, to the nearest hundredth. 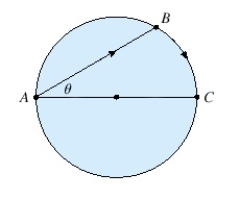
(Multiple Choice)
4.8/5  (30)
(30)
Use the guidelines of this section to sketch the curve. 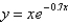 Select the graph of the curve.
Select the graph of the curve.
(Multiple Choice)
4.9/5  (38)
(38)
Use Newton's method with the specified initial approximation 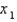 to find
to find 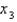 , the third approximation to the root of the given equation. (Round your answer to four decimal places.)
, the third approximation to the root of the given equation. (Round your answer to four decimal places.) 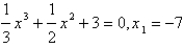
(Multiple Choice)
4.9/5  (37)
(37)
Showing 1 - 20 of 68
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)