Exam 9: Parametric Equations and Polar Coordinates
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Find the point(s) on the curve where the tangent is horizontal. 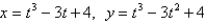
(Multiple Choice)
4.8/5  (33)
(33)
Select the curve by using the parametric equations to plot the points. 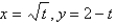
(Multiple Choice)
4.8/5  (31)
(31)
Set up, but do not evaluate, an integral that represents the length of the parametric curve. 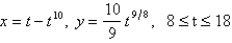
(Short Answer)
4.9/5  (33)
(33)
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. 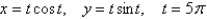
(Short Answer)
4.8/5  (42)
(42)
Write a polar equation in r and 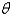 of a hyperbola with the focus at the origin, with the eccentricity
of a hyperbola with the focus at the origin, with the eccentricity 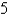 and directrix
and directrix 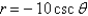 .
.
(Multiple Choice)
4.8/5  (41)
(41)
The planet Mercury travels in an elliptical orbit with eccentricity 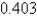 . Its minimum distance from the Sun is
. Its minimum distance from the Sun is 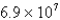 km. If the perihelion distance from a planet to the Sun is
km. If the perihelion distance from a planet to the Sun is 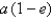 and the aphelion distance is
and the aphelion distance is 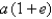 , find the maximum distance (in km) from Mercury to the Sun.
, find the maximum distance (in km) from Mercury to the Sun.
(Multiple Choice)
4.7/5  (30)
(30)
Write a polar equation of the conic that has a focus at the origin, eccentricity 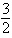 , and directrix
, and directrix 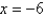 . Identify the conic.
. Identify the conic.
(Multiple Choice)
4.9/5  (41)
(41)
Write a polar equation in r and of an ellipse with the focus at the origin, with the eccentricity 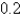 and vertex at
and vertex at 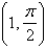 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Showing 21 - 30 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)