Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Write the slope-intercept form of the equation of the line through the given point parallel to the given line.
point: line:
(Multiple Choice)
4.8/5  (29)
(29)
Compare the graph of the following function with the graph of .
(Multiple Choice)
4.7/5  (25)
(25)
Determine the domain and range of the inverse function of the following function , where
(Multiple Choice)
4.9/5  (39)
(39)
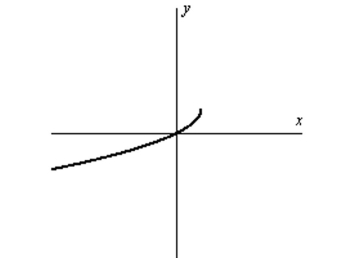
Determine an equation that may represented by the graph shown below.
(Multiple Choice)
4.8/5  (21)
(21)
Hooke's Law states that the force F required to compress or stretch a spring (within its elastic limits) is proportional to the distance d that the spring is compressed or stretched From its original length. That is, Fk= d, where k is the measure of the stiffness of the Spring and is called the spring constant. The table below shows the elongation d in Centimeters of a spring when a force of F kilograms is applied. Force, Elongation, 20 3.5 40 6.3 60 10.0 80 13.3 100 16.5
Find the equation of the line that seems to best fit the data.
(Multiple Choice)
5.0/5  (43)
(43)
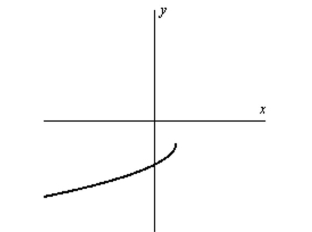
Determine an equation that may represented by the graph shown below.
(Multiple Choice)
4.8/5  (25)
(25)
Determine whether lines and passing through the pairs of points are parallel, perpendicular, or neither.
(Multiple Choice)
4.7/5  (34)
(34)
Determine the domain and range of the inverse function of the following function
, where
(Multiple Choice)
4.9/5  (32)
(32)
The scatter plots of different data are shown below. Determine whether there is a positive correlation, negative correlation, or no discernible correlation between the
Variables. 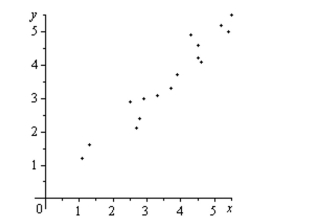
(Multiple Choice)
4.8/5  (36)
(36)
Algebraically determine whether the function below is even, odd, or neither.
(Multiple Choice)
4.8/5  (28)
(28)
Show algebraically that the functions and shown below are inverse functions.
(Multiple Choice)
4.7/5  (25)
(25)
Showing 81 - 100 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)