Exam 12: Review of Graphs, Equations, and Inequalities
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Rewrite as a rational function and find .
Free
(Multiple Choice)
4.7/5  (27)
(27)
Correct Answer:
D
Consider the following graph of the function and approximate , if it exists.
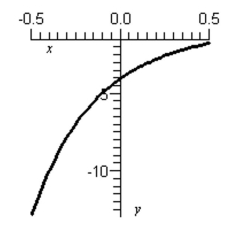
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
B
Use the figure below to approximate the slope of the curve at the point .
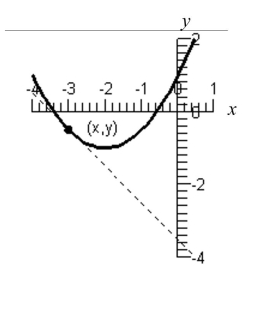
Free
(Multiple Choice)
4.7/5  (29)
(29)
Correct Answer:
E
Use the limit process to find the area of the region between and the -axis on the interval .
(Multiple Choice)
4.8/5  (42)
(42)
Use the derivative of to determine any points on the graph of at which the tangent line is horizontal.
(Multiple Choice)
4.9/5  (39)
(39)
Use the figure below to approximate the slope of the curve at the point .
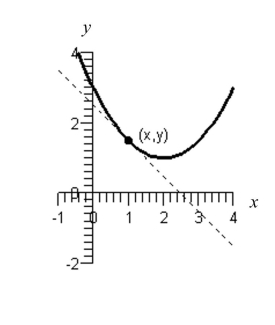
(Multiple Choice)
4.9/5  (41)
(41)
Use the figure below to approximate the slope of the curve at the point .
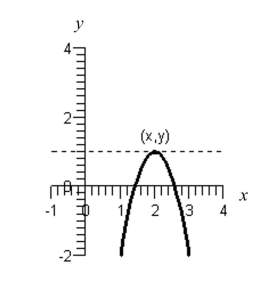
(Multiple Choice)
4.7/5  (38)
(38)
Let denote the midpoint of the line segment joining and . Find the distance from to the point . Round the answer to the nearest tenth.
(Multiple Choice)
4.9/5  (35)
(35)
Complete the table and use the result to estimate
numerically.
x -8.1 -8.01 -8.001 -8 -7.999 -7.99 -7.9 f(x) ?
(Multiple Choice)
4.9/5  (40)
(40)
Use the figure below to approximate the slope of the curve at the point .
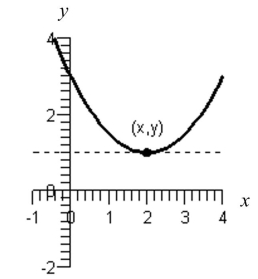
(Multiple Choice)
4.9/5  (29)
(29)
Showing 1 - 20 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)