Exam 10: Analytic Geometry in Three Dimensions
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Find a set of parametric equations for the line that passes through the given points. Show all your work.
(9,8, -2) ,(-3, -6,4)
Free
(Essay)
4.8/5  (38)
(38)
Correct Answer:
Answers may vary. One possible answer is shown below.
Find the angle between the two planes in degrees. Round to a tenth of a degree.
2x-y-4z=4 -3x-2y+4z=4
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
C
Find the area of the triangle with the given vertices.
Free
(Multiple Choice)
5.0/5  (44)
(44)
Correct Answer:
C
Find a set of parametric equations for the line that passes through the given points. Show all your work.
(Essay)
5.0/5  (37)
(37)
Find the torque on the crankshaft using the data shown in the figure. Round to the nearest tenth of a foot-pound.
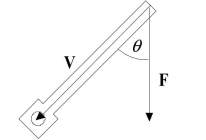 \|\|=1.6 \|\|=20 \theta=6
\|\|=1.6 \|\|=20 \theta=6
(Multiple Choice)
4.9/5  (44)
(44)
Find the area of the parallelogram that has the vectors as adjacent sides.
(Multiple Choice)
4.9/5  (36)
(36)
Find the volume of the parallelpiped with the given vertices. A(8,-5,-4),B(2,2,5),C(9,4,-12),D(3,11,-3) E(8,-6,-10),F(2,1,-1),G(9,3,-18),H(3,10,-9) )
(Multiple Choice)
4.8/5  (34)
(34)
Find the lengths of the sides of the right triangle whose vertices are located at the given points. Show that these lengths satisfy the Pythagorean Theorem. Show all of your work. )
(Essay)
4.8/5  (37)
(37)
Write the component form of the vector described below.
Initial point:
Terminal point:
(Multiple Choice)
4.8/5  (31)
(31)
Find the general form of the equation of the plane with the given characteristics. The plane passes through the point and is parallel to the -plane
(Multiple Choice)
4.9/5  (37)
(37)
Find the coordinates of the point located three units in front of the -plane, eight units to the right of the -plane, and five units above the -plane.
(Multiple Choice)
4.8/5  (35)
(35)
Find the coordinates of the point located four units in front of the -plane, nine units to the right of the -plane, and three units below the -plane.
(Multiple Choice)
4.8/5  (36)
(36)
Find symmetric equations for the line through the point and parallel to the specified line. Show all your work.
(Essay)
4.9/5  (32)
(32)
Find the general form of the equation of the plane passing through the point and perpendicular to the specified line.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)