Exam 6: Additional Topics in Trigonometry
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
In the figure below, , and . Use this information to solve the parallelogram for . The diagonals of the parallelogram are represented by and . Round answer to two decimal places.
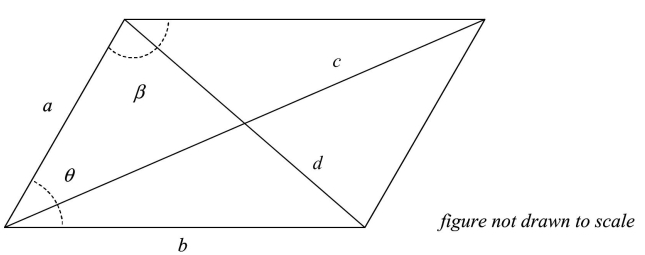
(Multiple Choice)
4.7/5  (36)
(36)
Determine whether and are orthogonal, parallel, or neither.
(Multiple Choice)
5.0/5  (36)
(36)
Given A =°16 , b =12 , and a = 10 , use the Law of Sines to solve the triangle (if possible) for the value of c. If two solutions exist, find both. Round answer to two
Decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Given vectors , and , determine whether the result of the following expression is a vector or a scalar.
(Multiple Choice)
4.7/5  (28)
(28)
Perform the operation below and leave the result in trigonometric form.
(Multiple Choice)
4.8/5  (39)
(39)
Use DeMoivre's Theorem to find the indicated power of the folllowing complex number.
(Multiple Choice)
4.7/5  (38)
(38)
Perform the operation shown below and leave the result in trigonometric form.
(Multiple Choice)
5.0/5  (35)
(35)
Find the trigonometric form of the complex number shown below.
(Multiple Choice)
4.8/5  (32)
(32)
Use DeMoivre's Theorem to find the indicated power of the following complex number.
(Multiple Choice)
4.9/5  (30)
(30)
Given vectors , and , determine whether the result of the following expression is a vector or a scalar.
(Multiple Choice)
4.8/5  (39)
(39)
Given , and , use the Law of Sines to solve the triangle for the value of . Round answer to two decimal places.
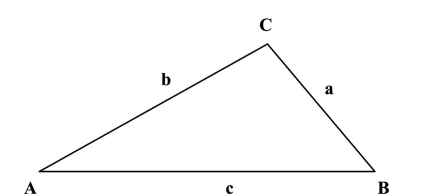
(Multiple Choice)
4.9/5  (31)
(31)
Determine whether and are orthogonal, parallel, or neither.
(Multiple Choice)
4.9/5  (34)
(34)
Find the vector that has a magnitude of 4 and is in the same direction as , where .
(Multiple Choice)
4.8/5  (27)
(27)
Use Heron's area formula to find the area of the triangle pictured below, if inches, inches, and inches.
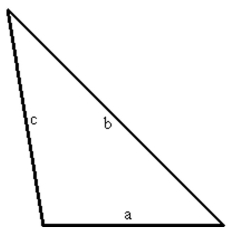
(Multiple Choice)
4.9/5  (40)
(40)
Find the fourth roots of . Write the roots in trigonometric form.
(Multiple Choice)
4.7/5  (28)
(28)
Find the vector v that has a magnitude of 4 and is in the same direction as u, where
(Multiple Choice)
4.9/5  (34)
(34)
A straight road makes an angle, , of with the horizontal. When the angle of elevation, , of the sun is , a vertical pole beside the road casts a shadow 8 feet long parallel to the road. Approximate the length of the pole. Round answer to two decimal places.
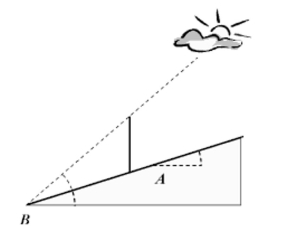
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)