Exam 12: Review of Graphs, Equations, and Inequalities
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
The average salary (in thousands of dollars) at a certain company for the first ten years of its existence can be approximated by the model . How many years did it take for the average salary to reach ?
Round the answer to the nearest hundredth of a year.
(Multiple Choice)
4.8/5  (34)
(34)
Use the limit process to find the slope of the graph of at .
(Multiple Choice)
5.0/5  (34)
(34)
Use the figure below to approximate the slope of the curve at the point .
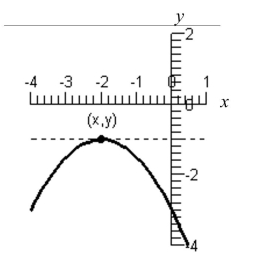
(Multiple Choice)
4.8/5  (33)
(33)
Determine any points on the graph of the following function at which the tangent line is horizontal.
(Multiple Choice)
4.9/5  (42)
(42)
Approximate the area of the region under the function below on the interval using 8 rectangles. Round your answer to two decimals.
(Multiple Choice)
4.8/5  (31)
(31)
Use the limit process to find the area of the region between and the -axis on the interval .
(Multiple Choice)
4.9/5  (41)
(41)
Consider the following graph of the function and approximate , if it exists.
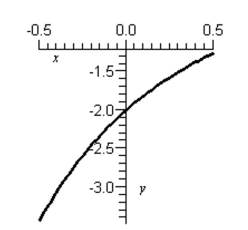
(Multiple Choice)
4.9/5  (35)
(35)
Approximate the area of the indicated region under the given curve using five rectangles.
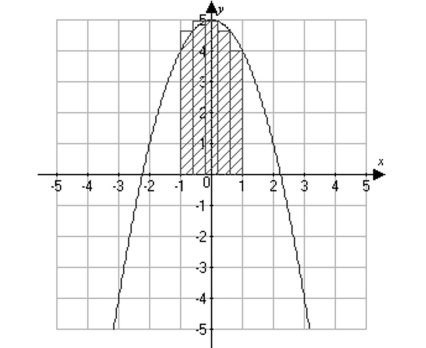
(Multiple Choice)
4.7/5  (38)
(38)
Find the coordinates of the point that is located 8 units below the -axis and 5 units to the left of the y-axis.
(Multiple Choice)
4.7/5  (27)
(27)
Determine any points on the graph of the following function at which the tangent line is horizontal.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 61 - 80 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)