Exam 15: Risk and Information
Exam 1: Analyzing Economic Problems79 Questions
Exam 2: Demand and Supply Analysis104 Questions
Exam 3: Consumer Preferences and the Concept of Utility88 Questions
Exam 4: Consumer Choice83 Questions
Exam 5: The Theory of Demand94 Questions
Exam 6: Inputs and Production Functions108 Questions
Exam 7: Costs and Cost Minimization84 Questions
Exam 8: Cost Curves91 Questions
Exam 9: Perfectly Competitive Markets86 Questions
Exam 10: Competitive Markets: Applications86 Questions
Exam 11: Monopoly and Monopsony83 Questions
Exam 12: Capturing Surplus79 Questions
Exam 13: Market Structure and Competition70 Questions
Exam 14: Game Theory and Strategic Behavior69 Questions
Exam 15: Risk and Information71 Questions
Exam 16: General Equilibrium Theory69 Questions
Exam 17: Externalities and Public Goods68 Questions
Select questions type
Large firms that can take on a number of small investment projects whose returns are independent of each other would most likely be characterized as:
(Multiple Choice)
4.9/5  (36)
(36)
A decision-maker is faced with a choice between a lottery with a 30% chance of a payoff of $30 and a 70% chance of a payoff of $80, and a guaranteed payoff of $65. If the decision maker's utility function is what is the risk premium associated with this choice?
(Multiple Choice)
4.7/5  (41)
(41)
Use the following decision tree to answer the next question.
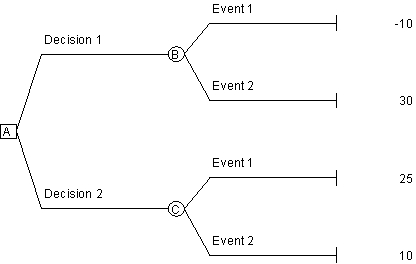 -In the decision tree above, for what probability of Event 1 will Decision 1 and Decision 2 have the same expected value?
-In the decision tree above, for what probability of Event 1 will Decision 1 and Decision 2 have the same expected value?
(Multiple Choice)
4.9/5  (43)
(43)
Consider a fairly-priced insurance policy that fully indemnifies the purchaser against their loss. This insurance policy would most likely be purchased by:
(Multiple Choice)
4.9/5  (34)
(34)
Suppose a fair, two-sided coin is flipped. If it comes up heads you receive $5; if it comes up tails you lose $1. The variance of this lottery is what?
(Multiple Choice)
4.9/5  (36)
(36)
Use the following probability distribution for a lottery to answer this question. 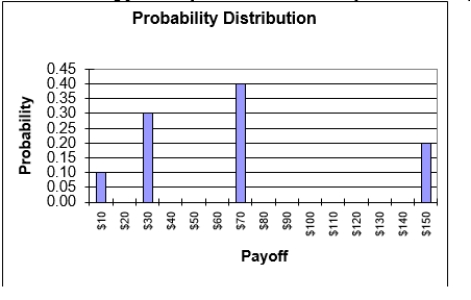 -Given the probability distribution for the lottery above, what is the expected value of this lottery?
-Given the probability distribution for the lottery above, what is the expected value of this lottery?
(Multiple Choice)
4.7/5  (34)
(34)
Heading: Analyzing Risky Decisions
**Reference: Use the decision tree along with the given probabilities to answer the next six questions
Probability Event A = 30% Probability Event B = 70%
Probability Event 1 = 58% Probability Event 2 = 42%
Probability of Event A given that Event 1 occurs = 16%
Probability of Event B given that Event 1 occurs = 84%
Probability of Event A given that Event 2 occurs = 50%
Probability of Event B given that Event 2 occurs = 50%
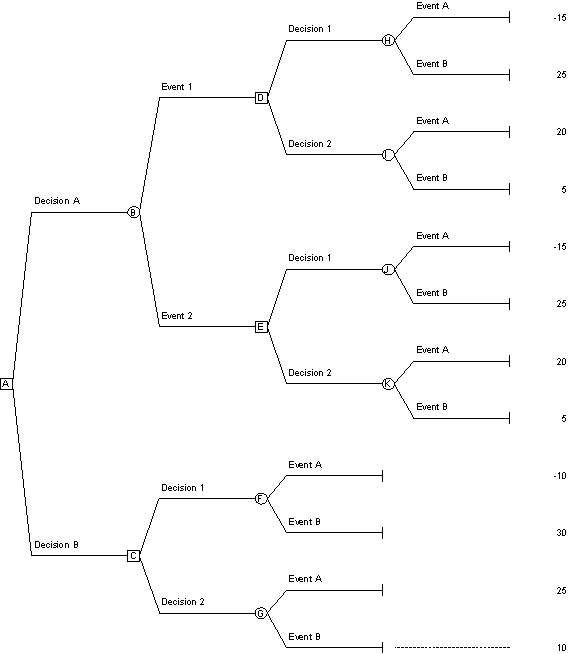 -*If the cost of obtaining information to determine Event 1 and Event 2 is $5, what is the value of perfect information?
-*If the cost of obtaining information to determine Event 1 and Event 2 is $5, what is the value of perfect information?
(Multiple Choice)
4.8/5  (45)
(45)
A decision maker has a utility function U = 10I. This decision maker is:
(Multiple Choice)
4.9/5  (38)
(38)
Would you expect an insurance company in the "real world" to sell an insurance policy for exactly the "fairly-priced" level as defined in the text?
(Multiple Choice)
5.0/5  (36)
(36)
 -Suppose you purchase a collectible baseball card from an acquaintance for $50. You think it could be worth $1,000 with a 10% probability and $0 with a 90% probability. What is your expected value for the baseball card?
-Suppose you purchase a collectible baseball card from an acquaintance for $50. You think it could be worth $1,000 with a 10% probability and $0 with a 90% probability. What is your expected value for the baseball card?
(Multiple Choice)
4.7/5  (30)
(30)
A risk-averse decision maker will choose the alternative with the lowest variance among alternatives with identical expected utilities.
(True/False)
4.8/5  (31)
(31)
What would be the expected value, variance and standard deviation of an event that always took the value one as its outcome?
(Multiple Choice)
4.8/5  (34)
(34)
Your current disposable income is $10,000. There is a 10% chance you will get in a serious car accident, incurring damage of $1,900. (There is a 90% chance that nothing will happen.)Your utility function is ,where I is income. If this policy is priced at $40, what is the change in your expected utility if you purchase the policy rather than no insurance?
(Multiple Choice)
4.9/5  (35)
(35)
Showing 21 - 40 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)