Exam 10: Characteristics of Functions and Their Graphs
Exam 1: Basic Concepts306 Questions
Exam 2: Equations and Inequalities234 Questions
Exam 3: Graphs and Functions61 Questions
Exam 4: Systems of Equations and Inequalities116 Questions
Exam 5: Polynomials and Polynomial Functions112 Questions
Exam 6: Rational Expressions and Equations130 Questions
Exam 7: Roots, Radicals, and Complex Numbers298 Questions
Exam 8: Quadratic Functions221 Questions
Exam 9: Exponential and Logarithmic Functions229 Questions
Exam 10: Characteristics of Functions and Their Graphs142 Questions
Exam 11: Conic Sections132 Questions
Exam 12: Sequences, Series, and Probability208 Questions
Select questions type
Determine the maximum possible number of turning points for the graph of the function.
-
(Multiple Choice)
4.7/5  (28)
(28)
Find all real zeros (estimate the irrational zeros to the nearest hundredth).
-
(Multiple Choice)
4.8/5  (34)
(34)
Use Descartes' Rule of Signs to determine the possible number of positive and negative real zeros for the polynomial
function.
-
(Multiple Choice)
4.9/5  (33)
(33)
Find the real zeros of the function, state their multiplicities if it is a number other than 1.
-
(Multiple Choice)
4.9/5  (37)
(37)
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
(Multiple Choice)
4.8/5  (42)
(42)
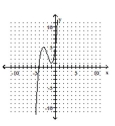
Identify the local maximum and minimum of the graphed function.
-
(Multiple Choice)
4.7/5  (41)
(41)
Determine whether the function is an even function, an odd function, or neither.
-
(Multiple Choice)
4.9/5  (29)
(29)
Describe the location, either above the x-axis or below the x-axis, of the graph of the function for large positive values of
x and for large negative values of x.
-
(Multiple Choice)
4.8/5  (47)
(47)
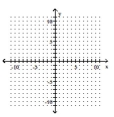
Determine the minimum degree of the polynomial function graphed.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use the Boundedness Theorem to determine if the zeros of f(x)are bounded over the given interval. If this cannot be
determined, indicate so.
-
(Multiple Choice)
4.9/5  (38)
(38)
Determine which of the given graphs could be the graph of the given polynomial function.
-
(Multiple Choice)
4.8/5  (32)
(32)
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
(Multiple Choice)
4.8/5  (29)
(29)
Classify the function as continuous or discontinuous. If the function is not continuous, identify the point(s)of
discontinuity.
-
(Multiple Choice)
4.8/5  (38)
(38)
Showing 81 - 100 of 142
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)