Exam 1: Functions and Graphs
Exam 1: Functions and Graphs224 Questions
Exam 2: Limits and the Derivative123 Questions
Exam 3: Additional Derivative Topics126 Questions
Exam 4: Graphing and Optimization116 Questions
Exam 5: Integration93 Questions
Exam 6: Additional Integration Topics82 Questions
Exam 7: Multivariable Calculus78 Questions
Exam 8: Trigonometric Functions92 Questions
Exam 9: Differential Equations47 Questions
Exam 10: Taylor Polynomials and Infinite Series48 Questions
Exam 11: Probability and Calculus57 Questions
Exam 12: Basic Algebra Review44 Questions
Exam 13: Special Topics20 Questions
Select questions type
Write an equation of the line with the indicated slope and y intercept.
-
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-If $4,000 is invested at 7% compounded annually, how long will it take for it to grow to $6,000, assuming no withdrawals are made? Compute answer to the next higher year if not exact. 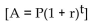
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-The financial department of a company that produces digital cameras arrived at the following price-demand
function and the corresponding revenue function: 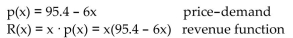 The function p(x) is the wholesale price per camera at which x million cameras can be sold and R(x) is the corresponding
revenue (in million dollars). Both functions have domain
The function p(x) is the wholesale price per camera at which x million cameras can be sold and R(x) is the corresponding
revenue (in million dollars). Both functions have domain 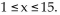 They also found the cost function to be C(x) = 150
+ 15.1x (in million dollars) for manufacturing and selling x cameras. Find the profit function and determine the
approximate number of cameras, rounded to the nearest hundredths, that should be sold for maximum profit.
They also found the cost function to be C(x) = 150
+ 15.1x (in million dollars) for manufacturing and selling x cameras. Find the profit function and determine the
approximate number of cameras, rounded to the nearest hundredths, that should be sold for maximum profit.
(Essay)
4.8/5  (28)
(28)
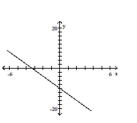
The graph that follows is the graph of a polynomial function. (i) What is the minimum degree of a polynomial function
that could have the graph? (ii) Is the leading coefficient of the polynomial negative or positive?
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Assume that a savings account earns interest at the rate of 2% compounded monthly. If this account contains $1000 now, how many months will it take for this amount to double if no withdrawals are made?
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The number of books in a community college library increases according to the function 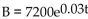 , where t is measured in years. How many books will the library have after 8 year(s)?
, where t is measured in years. How many books will the library have after 8 year(s)?
(Multiple Choice)
4.7/5  (42)
(42)
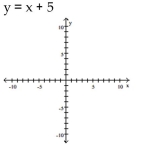
Use point-by-point plotting to sketch the graph of the equation.
-
(Multiple Choice)
4.7/5  (31)
(31)
Solve graphically to two decimal places using a graphing calculator.
-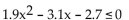
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-In the table below, the amount of the U.S. minimum wage is listed for selected years. 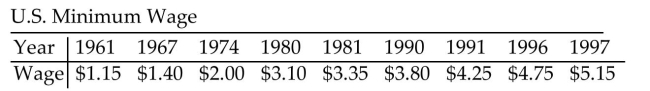 Find an exponential regression model of the form y = a ·bx, where y represents the U.S. minimum wage x years
after 1960. Round a and b to four decimal places. According to this model, what will the minimum wage be in
2005? In 2010?
Find an exponential regression model of the form y = a ·bx, where y represents the U.S. minimum wage x years
after 1960. Round a and b to four decimal places. According to this model, what will the minimum wage be in
2005? In 2010?
(Essay)
5.0/5  (37)
(37)
Write an equation for a function that has a graph with the given transformations.
-The shape of 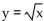 is shifted 5 units to the left. Then the graph is shifted 7 units upward.
is shifted 5 units to the left. Then the graph is shifted 7 units upward.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A small company that makes hand-sewn leather shoes has fixed costs of $320 a day, and total costs of $1200 per day at an output of 20 pairs of shoes per day. Assume that total cost C is linearly related to output x. Find an
Equation of the line relating output to cost. Write the final answer in the form C = mx + b.
(Multiple Choice)
4.8/5  (29)
(29)
Showing 121 - 140 of 224
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)