Exam 9: Matrices and Determinants
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Solve the problem.
-A basketball fieldhouse seats 15,000. Courtside seats sell for $9, end zone for $6, and balcony for $5. Total for a sell-out is $89,000. If half the courtside and balcony and all end zone seats are sold, ticket sales total $50,500.
How many of each type of seat are there?
(Multiple Choice)
4.8/5  (35)
(35)
Find a matrix A and a column matrix B that describe the following tables involving credits and tuition costs. Find the
matrix product AB, and interpret the significance of the entries of this product.
-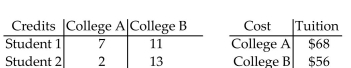
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Factory A makes 9 model-A, 5 model-D, and 8 model-M train sets. Factory B makes 11 model-A, 6 model-D, and 8 model-M train sets. If model-A sells for $15, model-D for $23, and model-M for $35, write a 2 x 3 matrix
To summarize the income by model.
(Multiple Choice)
4.8/5  (30)
(30)
Solve the system using the inverse of the coefficient matrix of the equivalent matrix equation.
-x + 3y = -8 -14x - 4y = -2
(Multiple Choice)
5.0/5  (28)
(28)
Solve the problem.
-Barnes and Able sell life, health, and auto insurance. Sales for May and June are given in the matrices. Life Health Auto  Find the matrix that would give total sales.
Find the matrix that would give total sales.
(Multiple Choice)
4.8/5  (40)
(40)
Solve the system of equations corresponding to the given matrix equation.
-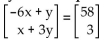
(Multiple Choice)
4.7/5  (32)
(32)
Solve the system, using Cramer's rule, if possible.
-5x - y + 5z = 73 6x + 6y - 8z = 12
-7x - 8y + z = -96
(Multiple Choice)
4.7/5  (29)
(29)
The size of two matrices is given. Find the size of the product AB and the product BA, if the products exist.
-A is 3 × 4, B is 4 × 3.
(Multiple Choice)
4.7/5  (32)
(32)
Given matrices A and B, find the indicated matrix if possible.
-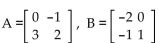 Find AB.
Find AB.
(Multiple Choice)
4.8/5  (24)
(24)
Solve the system using the inverse of the coefficient matrix of the equivalent matrix equation.
-0.3x - 0.4y - 0.1z = 9 -0.5x + 0.6y + 0.1z = -13
0.1x + 0.3y - 0.2z = 2
(Multiple Choice)
4.8/5  (29)
(29)
Showing 81 - 100 of 218
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)