Exam 6: Trigonometric Identities and Conditional Equations
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Find the exact value by using a sum or difference identity.
-tan 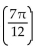
(Multiple Choice)
4.8/5  (21)
(21)
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Prove that the equation is an identity.
-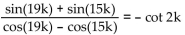
(Essay)
4.8/5  (35)
(35)
Use a half-angle identity to find an exact value for the following, given the information about x.
-Find cos 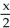 , given that sin
, given that sin 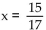 and 360° < x < 450°.
and 360° < x < 450°.
(Multiple Choice)
4.9/5  (39)
(39)
For the given function, determine the amplitude and find the phase shift.
-6 sin x - 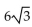 cos x Give the phase shift in radians in exact form.
cos x Give the phase shift in radians in exact form.
(Multiple Choice)
4.8/5  (40)
(40)
Find all real numbers in the interval 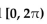 that satisfy the equation.
-2
that satisfy the equation.
-2 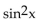 = sin x
= sin x
(Multiple Choice)
4.9/5  (27)
(27)
Graph the function by first writing it in the form y = A sin(x + C). State the amplitude, period, and phase shift.
-y = 3 sin x + 3 cos x 
(Multiple Choice)
5.0/5  (25)
(25)
Simplify the expression by using a sum or difference identity.
-cos(14k) cos (2k) - sin(14k) sin (2k)
(Multiple Choice)
5.0/5  (40)
(40)
Find the exact value of the expression using the provided information.
-Find tan(A + B) 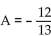 , with A in quadrant II, and sin
, with A in quadrant II, and sin 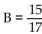 , with B in quadrant II.
, with B in quadrant II.
(Multiple Choice)
4.8/5  (39)
(39)
Find all values of x in the interval [0°, 360°) that satisfy the equation. Round approximate answers to the nearest tenth of a
degree.
-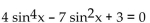
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A block hanging from a spring is free to oscillate. If a 1-kg block attached to the spring is given a downward velocity of 0.5 m/sec from a point 0.6 m above its resting position, then at any time t in seconds its position in
Meters is given by x = 0.5 sin t - 0.6 cos t. Find the maximum distance that the block travels from its resting
Position.
(Multiple Choice)
4.8/5  (34)
(34)
Find the exact value, given that sin A = -4/5 with A in quadrant IV, tan B = 7/24 with B in quadrant III, and cos C = - 5/13
with C in quadrant II.
-tan 2C
(Multiple Choice)
4.7/5  (37)
(37)
Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
-What happens when you try to evaluate 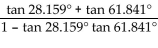 ?
?
(Essay)
4.8/5  (39)
(39)
Find all angles in [0°, 360°) that satisfy the equation.
-cos 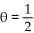
(Multiple Choice)
4.9/5  (29)
(29)
Show that the equation is not an identity by listing the value(s) of the variable from among 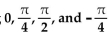 for which
the equation is false.
-
for which
the equation is false.
-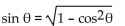
(Multiple Choice)
4.8/5  (35)
(35)
Showing 221 - 240 of 674
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)