Exam 6: Trigonometric Identities and Conditional Equations
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Use an identity to write the expression as a single trigonometric function or as a single number.
-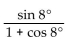
(Multiple Choice)
5.0/5  (43)
(43)
Write in terms of the cofunction of a complementary angle.
-csc (90° - 8°)
(Multiple Choice)
4.8/5  (34)
(34)
Prove that the equation is an identity.
-tan x + cot x = sec x csc x
(Essay)
4.8/5  (36)
(36)
Write the expression in terms of sines and/or cosines, and then simplify.
-sec x + csc x
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-A block hanging from a spring is free to oscillate. If a 1-kg block attached to the spring is given an upward velocity of 0.7 m/sec from a point 0.8 m below its resting position, then at any time t in seconds its position in
Meters is given by x = -0.7 sin t + 0.8 cos t. Find the maximum distance that the block travels from its resting
Position.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-A block hanging from a spring is free to oscillate. If a 1-kg block attached to the spring is given a downward velocity of 0.8 m/sec from a point 0.7 m below its resting position, then at any time t in seconds its position in
Meters is given by x = 0.8 sin t + 0.7 cos t. Find the maximum distance that the block travels from its resting
Position.
(Multiple Choice)
4.8/5  (38)
(38)
Find all real numbers in the interval 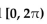 that satisfy the equation.
-
that satisfy the equation.
-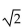 cos 2x = 1
cos 2x = 1
(Multiple Choice)
4.9/5  (33)
(33)
Find the exact value using a double-angle identity.
-cos(120°)
(Multiple Choice)
4.7/5  (32)
(32)
For the given function, determine the amplitude and find the phase shift.
-y = 15 sin x + 20 cos x Give the phase shift in radians rounded to the nearest thousandth.
(Multiple Choice)
4.7/5  (31)
(31)
Use a product-to-sum identity to rewrite the expression.
-cos(13k) cos (6k)
(Multiple Choice)
4.9/5  (35)
(35)
Find all real numbers in the interval 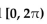 that satisfy the equation.
-cos x cos
that satisfy the equation.
-cos x cos 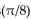 - sin x sin
- sin x sin 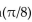 =
= 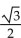
(Multiple Choice)
4.8/5  (46)
(46)
Write the expression in terms of sines and/or cosines, and then simplify.
-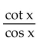
(Multiple Choice)
4.8/5  (40)
(40)
Find the exact value of the expression using the provided information.
-Find cos(A - B) 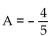 , with A in quadrant II, and cos
, with A in quadrant II, and cos 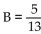 , with B in quadrant IV.
, with B in quadrant IV.
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether the function is odd, even, or neither.
-f( 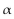 ) = 1 +
) = 1 + 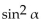
(Multiple Choice)
4.7/5  (35)
(35)
Showing 621 - 640 of 674
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)