Exam 1: Equations, Inequalities, and Modeling
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Solve the absolute value inequality. Write the solution set using interval notation.
-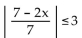
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-Decide whether or not the points are the vertices of a right triangle. (-1, 0), (1, 4), (3, 3)
(Multiple Choice)
4.7/5  (44)
(44)
Find the product of the complex number and its conjugate.
-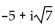
(Multiple Choice)
4.8/5  (40)
(40)
Use the square root property to find all real or imaginary solutions to the equation.
-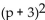 = 11
= 11
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-The value, v, in hundreds of dollars, of Juan's computer is approximated by 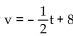 , where t is the number of years since he first bought the computer. Estimate the value of the computer 2 years after it was purchased.
, where t is the number of years since he first bought the computer. Estimate the value of the computer 2 years after it was purchased.
(Multiple Choice)
4.9/5  (32)
(32)
Write an inequality of the form ![Write an inequality of the form k or of the form k so that the inequality has the given solution set. -[-10, 10]](https://storage.examlex.com/TB8458/11ebc145_5dee_3bba_8acb_a53a9d7650f0_TB8458_11.jpg) k or of the form
k or of the form ![Write an inequality of the form k or of the form k so that the inequality has the given solution set. -[-10, 10]](https://storage.examlex.com/TB8458/11ebc145_5dee_3bbb_8acb_e987bc75c0af_TB8458_11.jpg) k so that the inequality has the given solution set.
-[-10, 10]
k so that the inequality has the given solution set.
-[-10, 10]
(Multiple Choice)
4.7/5  (38)
(38)
Use the scatter diagram to determine whether there is a linear relationship, a nonlinear relationship, or no relationship
between the variables.
-
(Multiple Choice)
4.9/5  (46)
(46)
Decide whether the given number is a solution to the equation preceding it.
-p + 11 = 25; 14
(Multiple Choice)
4.8/5  (29)
(29)
Use the square root property to find all real or imaginary solutions to the equation.
-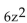 - 726 = 0
- 726 = 0
(Multiple Choice)
4.7/5  (48)
(48)
Solve the problem.
-A grasshopper is perched on a reed 5 inches above the ground. It hops off the reed and lands on the ground about 7.9 inches away. During its hop, its height is given by the equation 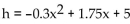 , where x is the
Distance in inches from the base of the reed, and h is in inches. How far was the grasshopper from the base of
The reed when it was 3.75 inches above the ground? Round to the nearest tenth.
, where x is the
Distance in inches from the base of the reed, and h is in inches. How far was the grasshopper from the base of
The reed when it was 3.75 inches above the ground? Round to the nearest tenth.
(Multiple Choice)
4.9/5  (31)
(31)
Find the real or imaginary solutions by using the quadratic formula.
-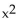 - 14x + 74 = 0
- 14x + 74 = 0
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-From a point on a straight road, John and Fred ride bicycles in opposite directions. John rides 10 miles per hour and Fred rides 13 miles per hour. In how many hours will they be 115 miles apart?
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-A repair company's charge for repairing a certain type of copy machine fits the model y = 47.38 + 0.617x where y is the number of dollars charged and x is the number of minutes the repair person is on the job. How many
Minutes would it take for the cost of repair to reach $120? (Round to the nearest minute.)
(Multiple Choice)
4.8/5  (37)
(37)
The distance d from the point 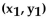 to the line Ax + By = C is given by the formula d
to the line Ax + By = C is given by the formula d 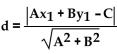 Find the exact
distance from the given point to the given line.
-(3, 6), y = 5x - 8
Find the exact
distance from the given point to the given line.
-(3, 6), y = 5x - 8
(Multiple Choice)
4.8/5  (28)
(28)
Use the square root property to find all real or imaginary solutions to the equation.
-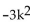 + 12 = 0
+ 12 = 0
(Multiple Choice)
5.0/5  (45)
(45)
Solve the problem.
-Janet drove 325 kilometers and the trip took 5 hours. How fast was Janet traveling?
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-Decide whether or not the points are the vertices of a right triangle. (7, 11), (13, 13), (19, 6)
(Multiple Choice)
4.9/5  (36)
(36)
For the equation in the form 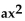 + bx + c = 0, determine the number of real solutions by examining the graph of
y =
+ bx + c = 0, determine the number of real solutions by examining the graph of
y = 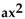 + bx + c.
-
+ bx + c.
-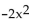 + 8x - 12 = 0
+ 8x - 12 = 0
(Multiple Choice)
4.8/5  (31)
(31)
Showing 221 - 240 of 531
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)