Exam 14: Developing Aspects of Proportional Reasoning: Ratio, Proportion, and Percent
Exam 1: Elementary Mathematics for the 21st Century10 Questions
Exam 2: Defining a Comprehensive Mathematics Program16 Questions
Exam 3: Mathematics for Every Child37 Questions
Exam 4: Learning Mathematics39 Questions
Exam 5: Organizing Effective Instruction37 Questions
Exam 6: Integrating Assessment41 Questions
Exam 7: Developing Problem-Solving Strategies43 Questions
Exam 8: Developing Concepts of Number42 Questions
Exam 9: Extending Number Concepts and Number Systems43 Questions
Exam 10: Developing Number Operations With Whole Numbers48 Questions
Exam 11: Extending Computational Fluency With Larger Numbers41 Questions
Exam 12: Developing Understanding of Common and Decimal Fractions45 Questions
Exam 13: Extending Understanding of Common and Decimal Fractions48 Questions
Exam 14: Developing Aspects of Proportional Reasoning: Ratio, Proportion, and Percent49 Questions
Exam 15: Thinking Algebraically43 Questions
Exam 16: Developing and Extending Geometric Concepts and Systems47 Questions
Exam 17: Developing and Extending Measurement Concepts44 Questions
Exam 18: Understanding and Representing Concepts of Data43 Questions
Exam 19: Investigating Probability47 Questions
Select questions type
A Canadian dollar is worth $0.90. How much is $10.00 worth in Canadian dollars?
(Multiple Choice)
4.8/5  (37)
(37)
The state that Mr. Smith lives in has a 6% sales tax. If he purchases a boat that costs $16,000, he must pay $960 in taxes. The correct term associated with the $960 is referred to as the:
(Multiple Choice)
4.9/5  (40)
(40)
Choose three of the meanings of ratios (part-whole sense, part-part-whole sense, relationship between two independent sets, ratio as a rate, probability relationships, or ratio as an operator)and explain the differences between them. Use examples to illustrate the differences.
(Essay)
4.9/5  (40)
(40)
A common misconception students have when working with similar figures in geometry is that they want to add the lengths of segments, rather than multiply. How could you convince a student that multiplication is the proper operation?
(Short Answer)
4.9/5  (42)
(42)
PISA: Trinity is in the hospital and receives an injection of penicillin. Her body gradually breaks the penicillin down so that one hour after the injection only 60% of the penicillin will remain. The pattern continues: At the end of each hour only 60% of the penicillin that was present at the end of the previous hour remains active. Suppose Trinity is given a dose of 300 milligrams of penicillin at 0800 hours. Complete this table showing the amount of penicillin that will remain active in Trinity's body at intervals of one hour from 0800 until 1100 hours.
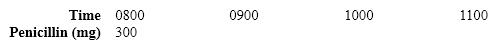
(Not Answered)
This question doesn't have any answer yet
All of the following are true about proportional reasoning except for :
(Multiple Choice)
4.7/5  (27)
(27)
Explain two of the inherent difficulties students have when learning proportional reasoning.
(Essay)
4.8/5  (40)
(40)
The price of a $5.00 hat is increased 20% to $6.00, then later, the hat is reduced back down to $5.00. Which of the following is a true statement?
(Multiple Choice)
4.9/5  (36)
(36)
Which equation can be used to solve the following problem:
A tire shop sold 55% of its inventory in the last year. If it sold 2,500 tires last year, how many tires did the tire shop have in stock last year?
(Multiple Choice)
4.7/5  (43)
(43)
Which equation could be used to solve the problem below?
The number of students in a school increased by 150. The school originally had 500 students. By what percent did the number of students increase?
(Multiple Choice)
4.8/5  (33)
(33)
A square made with all seven tangram pieces is 2. Write the size of each of the other pieces using common fractions, decimal fractions, and percent.
(Essay)
4.7/5  (33)
(33)
Explain the basic difference between using a rate table and using a multiples table when working with proportional reasoning.
(Essay)
4.8/5  (32)
(32)
TIMSS: If the ratio of 7 to 13 is the same as the ratio of x to 52, what is the value of x ?
(Multiple Choice)
4.8/5  (38)
(38)
Determining the chance of rolling a prime number (3:6)on a standard six-sided die with dots ranging from 1 to 6 is an example of which of the following meaning of ratios?
(Multiple Choice)
4.9/5  (37)
(37)
Explain how the "cross-product algorithm" for solving proportions can degrade students' understanding of proportional relationships.
(Essay)
4.8/5  (30)
(30)
Performance Tasks: Pattern Blocks and Tangrams
Use pattern blocks and tangrams to complete the tasks. Trace and mark your pieces to show your answers.
A square made with all seven tangram pieces is designated as one. Write the size of each of the pieces using common fractions, decimal fractions, and percent.
(Essay)
4.8/5  (33)
(33)
Which example below uses the meaning of ratio called ratio as an operator?
(Multiple Choice)
4.9/5  (32)
(32)
Teacher Licensing Examination Questions
NAEP: On the road shown below, the distance from Granville to Concord is 60 miles.
 What is the distance from Granville to Princeton?
What is the distance from Granville to Princeton?
(Multiple Choice)
4.7/5  (37)
(37)
Which option shows a between proportion based on the problem below?
Five shirts require 10 yards of cloth. How many yards of cloth will 15 shirts require?
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 49
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)