Exam 7: Vector Spaces
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
If S is a linearly independent subset of a vector space V, then S spans V.
(True/False)
4.9/5  (44)
(44)
If 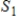 and
and 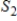 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 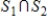 is an infinite-dimensional subspace of V.
is an infinite-dimensional subspace of V.
(True/False)
4.8/5  (44)
(44)
Find a basis for the subspace S of 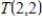 consisting of all linear transformations
consisting of all linear transformations 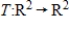 such that
such that
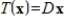 for some
for some 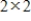 diagonal matrix D.
diagonal matrix D.
(Essay)
4.7/5  (36)
(36)
If every infinite set S in a vector space V is linearly dependent, then 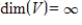 .
.
(True/False)
4.9/5  (35)
(35)
If S is a linearly independent subset of a vector space V, but S does not span V, then there exists a vector v in V such that the set 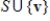 is also linearly independent.
is also linearly independent.
(True/False)
4.9/5  (27)
(27)
In the vector space 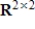 , let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of
, let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of 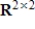 , and if not explain why.
, and if not explain why.
(Short Answer)
4.8/5  (29)
(29)
Every vector space V has a finite set S which both spans V and is linearly independent in V.
(True/False)
4.8/5  (44)
(44)
Determine the dimension of the subspace S of 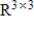 consisting of all symmetric matrices.
consisting of all symmetric matrices.
(Essay)
4.7/5  (40)
(40)
Find a basis for the subspace S of 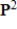 consisting of all polynomials p satisfying
consisting of all polynomials p satisfying 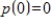 .
.
(Essay)
4.8/5  (33)
(33)
In the vector space 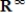 , let S be the set of all sequences
, let S be the set of all sequences 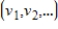 such that there exists some
such that there exists some 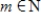 such that
such that 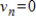 for all
for all 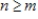 (all eventually-zero sequences). Determine if S is a subspace of
(all eventually-zero sequences). Determine if S is a subspace of 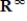 , and if not explain why.
, and if not explain why.
(Short Answer)
4.9/5  (45)
(45)
Determine the dimension of the subspace S of 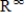 consisting of all sequences
consisting of all sequences 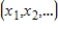 such that the series
such that the series 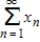 is convergent and satisfies
is convergent and satisfies 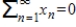 .
.
(Essay)
4.9/5  (44)
(44)
Find a basis for the subspace S of P consisting of all even polynomials, that is, all polynomials p satisfying 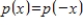 for all x.
for all x.
(Essay)
4.9/5  (42)
(42)
Showing 21 - 40 of 45
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)