Exam 4: Subspaces
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
If B1, B2 are bases for a given subspace, and A is the change of basis matrix from B1 to B2, then A is invertible, and
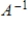 is the change of basis matrix from B2 to B1.
is the change of basis matrix from B2 to B1.
(True/False)
4.9/5  (40)
(40)
Find the change of basis matrix from the standard basis to B, and then convert x to the coordinate vector with respect to B. 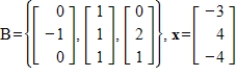
(Essay)
4.9/5  (41)
(41)
If B1, B2, and B3 are all bases for a given subspace, A is the change of basis matrix from B1 to B2, and B is the change of basis matrix from B2 to B3, then the change of basis matrix from B1 to B3 is given by BA.
(True/False)
4.8/5  (35)
(35)
Let
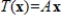 for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T.
for the matrix A. Determine if the vector b is in the kernel of T and if the vector c is in the range of T. 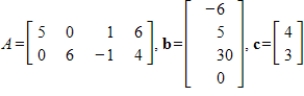
(Short Answer)
4.7/5  (30)
(30)
By forming matrix rows, find a basis for the given subspace S and give the dimension of S, where
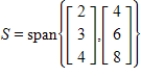
(Essay)
4.9/5  (41)
(41)
By forming matrix columns, find a basis for the given subspace S and give the dimension of S, where
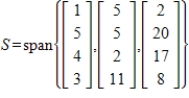
(Essay)
4.9/5  (40)
(40)
By forming matrix rows, find a basis for the given subspace S and give the dimension of S, where
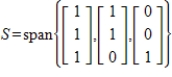
(Essay)
5.0/5  (43)
(43)
Determine if S is a subspace of R2, where S is the subset consisting of all vectors
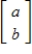 where
where
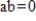 .
.
(Short Answer)
4.8/5  (41)
(41)
Determine if S is a subspace of R, where S is the subset consisting of all vectors
 where q is a rational number.
where q is a rational number.
(Short Answer)
4.9/5  (30)
(30)
Find bases for the column space of A, the row space of A, and the null space of A. 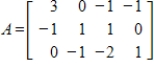
(Essay)
4.8/5  (34)
(34)
If T is an onto linear transformation from R3 to R5, and A is a matrix such that
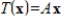 , then
, then
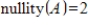 .
.
(True/False)
4.7/5  (44)
(44)
If T is a one-to-one linear transformation from R3 to R5, and A is a matrix such that
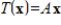 , then
, then
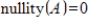 .
.
(True/False)
4.8/5  (40)
(40)
If E is an
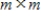 elementary matrix and A is an
elementary matrix and A is an
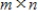 matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
matrix, then the subspace spanned by the rows of A is the same as the subspace spanned by the rows of EA.
(True/False)
4.9/5  (37)
(37)
Determine if S is a subspace of R3, where S is the subset consisting of all vectors
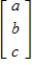 where
where
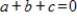 .
.
(Short Answer)
4.7/5  (31)
(31)
Showing 41 - 60 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)