Question 1

Geographically weighted regression builds a regression model for each observation in the data set.

Accepted Answer

A) True 
 B)False  True

Question 2

Explain the difference between "crisp threshold values" and "fuzzy sets" in multicriteria evaluation.

Accepted Answer

In multicriteria evaluation, "crisp threshold values" and "fuzzy sets" are two different approaches used to handle uncertainty and vagueness in decision-making processes.

Crisp threshold values are used in traditional decision-making methods where a clear and precise cutoff point is defined to separate different categories or classes. For example, in a binary classification problem, a crisp threshold value might be set to distinguish between "acceptable" and "unacceptable" options based on a specific criterion. This approach assumes that the data is precise and that there is no ambiguity in the decision-making process.

On the other hand, fuzzy sets allow for a more flexible and nuanced representation of uncertainty. Instead of using strict cutoff points, fuzzy sets allow for the gradual transition between different categories. This means that an option can belong to multiple categories to varying degrees, reflecting the inherent vagueness in real-world decision-making. Fuzzy sets are particularly useful when dealing with subjective or imprecise data, as they can capture the uncertainty and ambiguity present in the decision-making process.

In summary, the main difference between crisp threshold values and fuzzy sets lies in their treatment of uncertainty. Crisp threshold values rely on clear cutoff points and precise categorization, while fuzzy sets allow for a more flexible and nuanced representation of uncertainty, making them more suitable for handling complex and ambiguous decision-making scenarios in multicriteria evaluation.

Question 3

How does an index model differ from a binary model?

Accepted Answer

An index model and a binary model are two different types of models used in various fields such as finance, statistics, and computer science. They serve different purposes and are based on different principles. Here's how they differ:

Index Model:
1. An index model is used to describe the relationship between the return on a specific asset and the return on a market index. It is commonly used in finance, particularly in the Capital Asset Pricing Model (CAPM).
2. The index model assumes that the return on an asset is partly due to the market return and partly due to factors unique to the asset itself.
3. The model typically includes a systematic risk component represented by the market index and an unsystematic risk component that is asset-specific.
4. The index model can be represented by a linear equation: Ri = αi + βiRm + εi, where Ri is the return on asset i, αi is the asset's expected return independent of the market, βi is the asset's sensitivity to the market index (Rm), and εi is the random error term.
5. The index model is continuous in nature, meaning that the returns can take on any value within a range.

Binary Model:
1. A binary model, on the other hand, is used to predict outcomes that have two possible states, often referred to as "success" and "failure" or "1" and "0". It is widely used in fields like statistics, machine learning, and decision-making.
2. The binary model is used for classification purposes, where the goal is to categorize observations into one of two distinct groups.
3. This model does not typically involve a market index or any continuous variable as a predictor. Instead, it uses one or more independent variables to predict a binary outcome.
4. A common example of a binary model is logistic regression, where the probability of the outcome is modeled as a logistic function of the independent variables: P(Y=1) = 1 / (1 + e^-(β0 + β1X1 + ... + βnXn)).
5. The binary model is discrete in nature, as it deals with categorical outcomes rather than a continuous range of values.

In summary, an index model is used to explain the relationship between an asset's return and the market return, incorporating both systematic and unsystematic risk factors. It deals with continuous data and is often used in the context of financial markets. A binary model, on the other hand, is used for classification tasks with two possible outcomes and is applicable in various fields where such predictions are necessary. It deals with categorical, discrete data.

Question 4

Many index models use the weighted linear combination method to calculate the index value. Explain the steps one follows in using the weighted linear combination method.

Accepted Answer

The weighted linear combination method i

Question 5

The output of an index model is a:

Accepted Answer

A)  true or false map 
B)  ranked map 
A)  true or false map 
B)  ranked map

Question 6

An environmental model such as a soil erosion model must be capable of dealing with the interaction of many variables including physical and cultural variables.

Accepted Answer

A) True 
 B)False

Question 7

Briefly describe the process of model calibration.

Accepted Answer

Model calibration is a process in which

Question 8

The output of a site analysis is typically a binary map.

Accepted Answer

A) True 
 B)False

Question 9

How does a static model differ from a dynamic model?

Accepted Answer

A static model and a dynamic model are t

Question 10

Which of the following analyses commonly uses index models?

Accepted Answer

A)  a and c 
B)  site analysis 
C)  vulnerability analysis 
D)  b and c 
E)  suitability analysis 
A)  a and c 
B)  site analysis 
C)  vulnerability analysis 
D)  b and c 
E)  suitability analysis

Question 11

To build an index model, one must assign a(n) ____ to each variable or factor under consideration:

Accepted Answer

A)  numeric score 
B)  ID 
C)  weight 
A)  numeric score 
B)  ID 
C)  weight

Question 12

Explain the usefulness of regression models for spatial data.

Accepted Answer

Regression models are extremely useful f

Question 13

In many instances, one can build a GIS model that is either vector-based or raster-based. What general guidelines should one use in deciding which type of model to build?

Accepted Answer

When deciding whether to build a vector-

Question 14

Which method is used by RUSLE to compute the average soil loss from six factors?

Accepted Answer

A)  addition of the six factors 
B)  multiplication of the six factors 
C)  weighted linear combination of the six factors 
A)  addition of the six factors 
B)  multiplication of the six factors 
C)  weighted linear combination of the six factors

Question 15

A common approach to building a vector-based binary model is to

Accepted Answer

A)  perform attribute data manipulation and analysis and overlay simultaneously 
B)  perform overlay first, followed by attribute data manipulation and analysis 
C)  perform attribute data manipulation and analysis first, followed by overlay 
A)  perform attribute data manipulation and analysis and overlay simultaneously 
B)  perform overlay first, followed by attribute data manipulation and analysis 
C)  perform attribute data manipulation and analysis first, followed by overlay

Question 16

A number of alternatives to the weighted linear combination method have been proposed in the literature. Describe one such alternative.

Accepted Answer

One alternative to the weighted linear c

Question 17

It is recommended that data sets used for validating a model are different from those for developing the model.

Accepted Answer

A) True 
 B)False

Question 18

You are asked to develop a vector-based index model. The model computes the index value using elevation and slope:
Index value = 2 * elevation + slope
The scoring (data standardization) systems for elevation and slope are as follows:
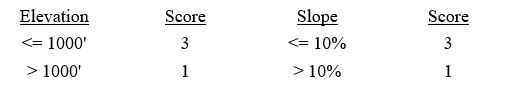   You already have the elevation and slope layers. Describe the procedure you will follow to complete the task.

Accepted Answer

The answer of You are asked to develop a vector-based...

Question 19

A model that offers prediction of what the conditions of geospatial data could be or should be is called a

Accepted Answer

A)  dynamic model 
B)  prescriptive model 
C)  deterministic model 
D)  static model 
A)  dynamic model 
B)  prescriptive model 
C)  deterministic model 
D)  static model

Question 20

How does a deterministic model differ from a stochastic model?

Accepted Answer

A deterministic model and a stochastic m

Geographically weighted regression builds a regression model for each observation in the data set.

Explain the difference between "crisp threshold values" and "fuzzy sets" in multicriteria evaluation.

How does an index model differ from a binary model?

Many index models use the weighted linear combination method to calculate the index value. Explain the steps one follows in using the weighted linear combination method.

The output of an index model is a:

An environmental model such as a soil erosion model must be capable of dealing with the interaction of many variables including physical and cultural variables.

Briefly describe the process of model calibration.

The output of a site analysis is typically a binary map.

How does a static model differ from a dynamic model?

Which of the following analyses commonly uses index models?

To build an index model, one must assign a(n) ____ to each variable or factor under consideration:

Explain the usefulness of regression models for spatial data.

In many instances, one can build a GIS model that is either vector-based or raster-based. What general guidelines should one use in deciding which type of model to build?

Which method is used by RUSLE to compute the average soil loss from six factors?

A common approach to building a vector-based binary model is to

A number of alternatives to the weighted linear combination method have been proposed in the literature. Describe one such alternative.

It is recommended that data sets used for validating a model are different from those for developing the model.

A model that offers prediction of what the conditions of geospatial data could be or should be is called a

How does a deterministic model differ from a stochastic model?

Introduction

Coordinate Systems

Vector Data Model

Raster Data Model

GIS Data Acquisition

Geometric Transformation

Spatial Data Accuracy and Quality

Attribute Data Management

Data Display and Cartography

Data Exploration

Vector Data Analysis

Raster Data Analysis

Terrain Mapping and Analysis

Viewshed and Watershed Analysis

Spatial Interpolation

Geocoding and Dynamic Segmentation

Least Cost Path and Network Analysis

Filters

Exam 18: GIS Models and Modeling

Geographically weighted regression builds a regression model for each observation in the data set.

Explain the difference between "crisp threshold values" and "fuzzy sets" in multicriteria evaluation.

How does an index model differ from a binary model?

Many index models use the weighted linear combination method to calculate the index value. Explain the steps one follows in using the weighted linear combination method.

The output of an index model is a:

An environmental model such as a soil erosion model must be capable of dealing with the interaction of many variables including physical and cultural variables.

Briefly describe the process of model calibration.

The output of a site analysis is typically a binary map.

How does a static model differ from a dynamic model?

Which of the following analyses commonly uses index models?

To build an index model, one must assign a(n) ____ to each variable or factor under consideration:

Explain the usefulness of regression models for spatial data.

In many instances, one can build a GIS model that is either vector-based or raster-based. What general guidelines should one use in deciding which type of model to build?

Which method is used by RUSLE to compute the average soil loss from six factors?

A common approach to building a vector-based binary model is to

A number of alternatives to the weighted linear combination method have been proposed in the literature. Describe one such alternative.

It is recommended that data sets used for validating a model are different from those for developing the model.

A model that offers prediction of what the conditions of geospatial data could be or should be is called a

How does a deterministic model differ from a stochastic model?

Introduction

Coordinate Systems

Vector Data Model

Raster Data Model

GIS Data Acquisition

Geometric Transformation

Spatial Data Accuracy and Quality

Attribute Data Management

Data Display and Cartography

Data Exploration

Vector Data Analysis

Raster Data Analysis

Terrain Mapping and Analysis

Viewshed and Watershed Analysis

Spatial Interpolation

Geocoding and Dynamic Segmentation

Least Cost Path and Network Analysis

Filters