Exam 9: Trigonometric Identities and Equations
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
Solve each equation or inequality over the indicated interval.
-
Free
(Short Answer)
4.8/5  (31)
(31)
Correct Answer:
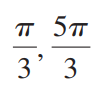
Given with and , find the exact values for the following:
-
Free
(Short Answer)
4.8/5  (29)
(29)
Correct Answer:
Suppose that the formula describes the motion formed by a rhythmically moving arm during an 8-minute time period where is the angle (in radians) formed by the arm at time (in minutes).
(a) Give the domain and range of .
(b) Graph over its domain.
(c) Use the graph to determine the maximum and minimum values of and when they occur.
(d) Find analytically and check your result graphically. Use symmetry to find .
(e) When is the angle radians?
(f) Write the equation as an equation involving arcsine by solving for .
Free
(Essay)
4.8/5  (39)
(39)
Correct Answer:
domain: ; range:
(b)
![domain: [0,8] ; range: \left[\frac{1}{3}, 1\right] (b) (c) maximum: 1 radians at t=2 minimum: \frac{1}{3} radian at t=6 (d) A(1)=\frac{4+\sqrt{2}}{6} ; A(6)=\frac{4+\sqrt{2}}{6} (e) A(t)=\frac{1}{2} at t=0, t=4 and t=8 (f) t=\frac{4}{\pi} \arcsin (3 A-2)](https://storage.examlex.com/TB9423/11eeb053_0833_ca7b_be9b_17fd36a7aa0b_TB9423_00.jpg)
(c) maximum: 1 radians at
minimum: radian at
(d)
(e) at and
(f)
Graph , and use the graph to conjecture an identity. Verify your conjecture analytically.
(Essay)
4.8/5  (27)
(27)
Graph , and use the graph to conjecture an identity. Verify your conjecture analytically.
(Essay)
4.8/5  (35)
(35)
Graph , and use the graph to conjecture an identity. Verify your conjecture analytically.
(Essay)
4.8/5  (45)
(45)
Solve each equation or inequality over the indicated interval.
-
(Short Answer)
4.8/5  (37)
(37)
Use an identity to write each expression as a trigonometric function of alone.
-
(Short Answer)
4.8/5  (33)
(33)
Use an identity to write each expression as a trigonometric function of alone.
-
(Short Answer)
4.8/5  (37)
(37)
Solve each equation or inequality over the indicated interval.
-
(Short Answer)
4.9/5  (48)
(48)
Solve each equation or inequality over the indicated interval.
-
(Short Answer)
4.8/5  (39)
(39)
Suppose that the formula describes the motion formed by a rhythmically moving arm during a 16 minute time period where is the angle (in radians) formed by the arm at time (in minutes).
(a) Give the domain and range of .
(b) Graph over its domain.
(c) Use the graph to determine the maximum and minimum values of and when they occur.
(d) Find analytically and check your result graphically. Use symmetry to find .
(e) When is the angle radians?
(f) Write the equation as an equation involving arcsine by solving for .
(Essay)
4.8/5  (35)
(35)
Showing 1 - 20 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)