Exam 7: Analytic Geometry and Nonlinear Systems
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
Consider the system of equations
x-3y+2z =5 2x-4y+3z =12 3x-7y+6z =23
(a) Write the matrix of coefficients , the matrix of variables , and the matrix of constants for this system.
(b) Find .
(c) Use the matrix inverse method to solve the system.
(d) If the matrix of constants is replaced by the matrix , find the solution to .
Free
(Essay)
4.9/5  (37)
(37)
Correct Answer:
(a)
(b)
(c)
(d)
Suppose that is a matrix and is a matrix.
(a) Can be found? If so, give the dimensions of the resulting matrix.
(b) Can be found? If so, give the dimensions of the resulting matrix.
(c) Does ? Explain why or why not.
(d) If and are each square matrices, will always exist?
Free
(Essay)
4.8/5  (42)
(42)
Correct Answer:
(a) Yes;
(b) Yes;
(c) No; They have different dimensions.
(d) No; and must have the same dimensions.
Find the partial fraction decomposition for the rational expression .
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
The solution set of a system of inequalities is shown below. Which of the following systems is it?
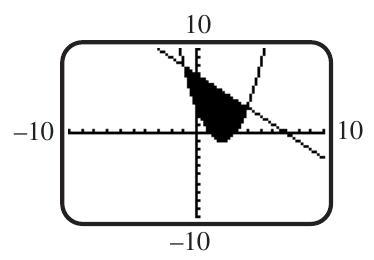 (a)
(b)
(c) y+x\geq7 y\leq-4x+3
(d)
(a)
(b)
(c) y+x\geq7 y\leq-4x+3
(d)
(Short Answer)
4.9/5  (29)
(29)
Find the partial fraction decomposition for the rational expression .
(Short Answer)
4.7/5  (34)
(34)
Find the partial fraction decomposition for the rational expression .
(Short Answer)
4.9/5  (28)
(28)
Consider the system of equations
3+4y =12 -9x+2y =-18
(a) What type of graph does each equation have?
(b) How many points of intersection are possible for these types of graphs?
(c) Solve the system.
(d) Support the solutions using a graphing calculator.
(Essay)
4.9/5  (34)
(34)
The minimum yearly temperature in a certain temperate climate was recorded each year for five years beginning
in 2000. The minimum temperature increased for the first few years before declining. The table shows the temperature, in degrees Fahrenheit, for those years, with 2000 represented by year 0, 2001 by year 1, and so on. Use the data points , and to find a quadratic function defined by that models the data. Graph together with the data.

(Essay)
4.7/5  (38)
(38)
Consider the system of equations
(a) Write the matrix of coefficients , the matrix of variables , and the matrix of constants for this system.
(b) Find .
(c) Use the matrix inverse method to solve the system.
(d) If the matrix of constants is replaced by the matrix , find the solution to .
(Essay)
4.8/5  (31)
(31)
The employment rate in a city has been documented at two year intervals. The table shows the number of employed citizens, in millions, tor several years, with 2000 represented by year 0,2002 by year 2 , and so on. Use the data points , and to find a quadratic function defined by that models the data. Graph together with the data.

(Essay)
4.8/5  (37)
(37)
Consider the system of equations
(a) What type of graph does each equation have?
(b) How many points of intersection are possible for these types of graphs?
(c) Solve the system.
(d) Support the solutions using a graphing calculator.
(Essay)
4.9/5  (33)
(33)
Suppose that is a matrix and is a matrix.
(a) Can be found? If so, give the dimensions of the resulting matrix.
(b) Can be found? If so, give the dimensions of the resulting matrix.
(c) Does ? Explain why or why not.
(d) If and are each square matrices, will always exist?
(Essay)
4.8/5  (30)
(30)
Showing 1 - 20 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)