Exam 5: Inverse, Exponential, and Logarithmic Functions
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
solve each equation. Give the solution set (a) with an exact value and then (b) with an approximation to the nearest thousandth.
-
Free
(Short Answer)
4.9/5  (43)
(43)
Correct Answer:
(a)
(b)
Consider the equation .
(a) Solve the equation analytically. If there is an extraneous value, what is it?
(b) To support the solution in part (a), we may graph and find the -intercept.
Write an expression for using the change-of-base rule with base 10 , and graph the function to support the solution from part (a).
(c) Use the graph to solve the inequality .
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
(a) ; the extraneous value is .
(b)
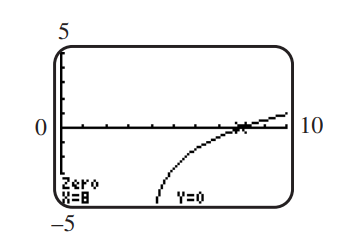
(c)
The concentration of pollutants in a stream is given by , where is the amount of pollutant in grams per liter and is the distance, in kilometers, downstream from the source of the pollution. Match each question with one of the solutions A, B, C, or D.
-How far downstream is the pollutant level equal to ?
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
An unstable radioactive isotope decays according to the equation where is the number of grams remaining and is the time measured in minutes. Match each question with one of the solutions A, B, C, or D.
-How long will it take for the material to decay to half its initial amount?
(Multiple Choice)
4.9/5  (38)
(38)
Consider the equation .
(a) Solve the equation analytically. If there is an extraneous value, what is it?
(b) To support the solution in part (a), we may graph and find the -intercept.
Write an expression for using the change-of-base rule with base 10, and graph the function to support the solution from part (a).
(c) Use the graph to solve the inequality .
(Essay)
4.8/5  (40)
(40)
solve each equation. Give the solution set (a) with an exact value and then (b) with an approximation to the nearest thousandth.
-
(Short Answer)
4.9/5  (38)
(38)
Use the power, quotient, and product properties of logarithms to write as an equivalent expression.
(Short Answer)
4.8/5  (29)
(29)
solve each equation. Give the solution set (a) with an exact value and then (b) with an approximation to the nearest thousandth.
-
(Short Answer)
4.7/5  (21)
(21)
Use the power, quotient, and product properties of logarithms to write as an equivalent expression.
(Short Answer)
4.8/5  (30)
(30)
A sample of radioactive material has a half-life of about 1250 years. An initial sample weighs 12 grams.
(a) Find a formula for the decay function for this material.
(b) Find the amount left after 5000 years.
(c) Find the time for the initial amount to decay to 3 grams.
(Short Answer)
4.9/5  (32)
(32)
Use a calculator to find an approximation of each logarithm to the nearest thousandth.
(a)
(b)
(c)
(Short Answer)
4.8/5  (39)
(39)
Suppose that is invested at for 12 years. Find the total amount present at the end of thime period if the interest is compounded (a) quarterly and (b) continuously.
(Short Answer)
4.9/5  (40)
(40)
One of your friends is taking another mathematics course and tells you, "I have no idea what an expression like really means." Write an explanation of what it means, and tell how you can find an approximation for it with a calculator.
(Essay)
4.8/5  (31)
(31)
Showing 1 - 20 of 84
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)