Exam 8: Numerical Methods
Exam 1: Introduction28 Questions
Exam 2: First-Order Differential Equations73 Questions
Exam 3: Second-Order Linear Differential Equations119 Questions
Exam 4: Higher-Order Linear Differential Equations54 Questions
Exam 5: Series Solutions of Second-Order Linear Equations81 Questions
Exam 6: The Laplace Transform57 Questions
Exam 7: Systems of First-Order Linear Equations97 Questions
Exam 8: Numerical Methods63 Questions
Exam 9: Nonlinear Differential Equations and Stability76 Questions
Exam 10: Partial Differential Equations and Fourier Series44 Questions
Exam 11: Boundary Value Problems and Sturm-Liouville Theory19 Questions
Select questions type
Consider the initial value problem
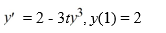 This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
How many approximations Yn are needed to estimate a solution at y(1.1) if h = 0.05?
n = ________
This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
How many approximations Yn are needed to estimate a solution at y(1.1) if h = 0.05?
n = ________
(Short Answer)
4.8/5  (42)
(42)
Consider the system of initial value problems given by
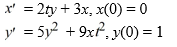 This problem can be expressed using matrix notation as
This problem can be expressed using matrix notation as
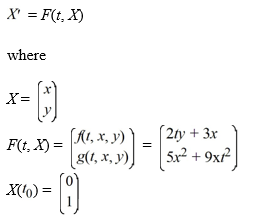 When using the Euler method with h = 0.1,
When using the Euler method with h = 0.1, 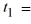 = ________
= ________
(Short Answer)
4.8/5  (37)
(37)
Consider the initial value problem
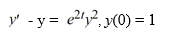 (Note: The exact solution is
(Note: The exact solution is 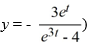 The size of the error eK is large because
The size of the error eK is large because
(Multiple Choice)
4.9/5  (39)
(39)
Consider the following initial value problem
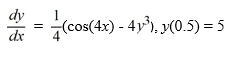 The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
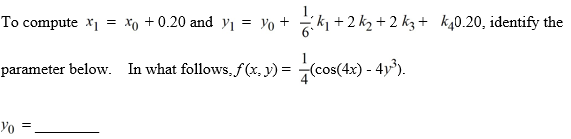
(Short Answer)
4.8/5  (33)
(33)
Consider the system of initial value problems given by
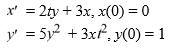 This problem can be expressed using matrix notation as
This problem can be expressed using matrix notation as
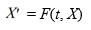 where
where
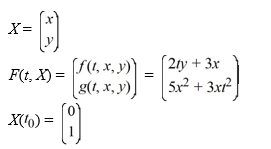 When using the Euler method with h = 0.1, t2 = ________
When using the Euler method with h = 0.1, t2 = ________
(Short Answer)
4.8/5  (39)
(39)
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 57.2 tanh(0.12t), t 3.0, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 3.05 seconds.Using a step size of h = 0.05 seconds, compute the vertical distance traveled in the first 3.05 seconds.
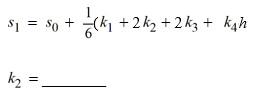
(Multiple Choice)
4.7/5  (39)
(39)
Consider the initial value problem
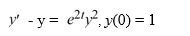 (Note: The exact solution is
(Note: The exact solution is 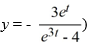 Which of the following expressions represents the error in the estimation for the improved Euler method?
E4 = ________
Which of the following expressions represents the error in the estimation for the improved Euler method?
E4 = ________
(Multiple Choice)
4.7/5  (33)
(33)
Given the initial value problem 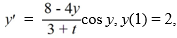 how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?
n = ________
how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?
n = ________
(Short Answer)
4.8/5  (30)
(30)
Consider the system of initial value problems given by
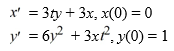 This problem can be expressed using matrix notation as
This problem can be expressed using matrix notation as
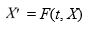 where
where
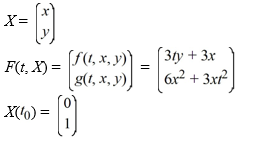 When using the improved Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution yn at t = 0.10?
n = ________
When using the improved Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution yn at t = 0.10?
n = ________
(Short Answer)
4.8/5  (34)
(34)
Consider the following initial value problem
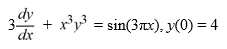 How would you need to rewrite this problem in order to apply the Runge-Kutta 4th order method to approximate the solution of this problem at a value of x?
How would you need to rewrite this problem in order to apply the Runge-Kutta 4th order method to approximate the solution of this problem at a value of x?
(Multiple Choice)
4.8/5  (38)
(38)
Consider the system of initial value problems given by
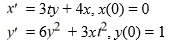 This problem can be expressed using matrix notation as
This problem can be expressed using matrix notation as
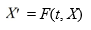 Where
Where
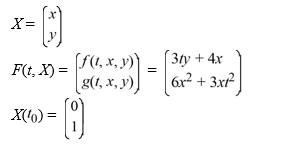 When using the Euler method with h = 0.05, what are the values of
When using the Euler method with h = 0.05, what are the values of 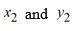 when using the Euler method?
when using the Euler method?
(Multiple Choice)
4.8/5  (36)
(36)
Consider the initial value problem 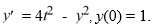 This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h = 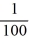 Y1 = ________
Y1 = ________
(Short Answer)
4.8/5  (39)
(39)
Consider the initial value problem 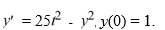 This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.
Which of these equations is the result of applying the backward Euler method to solve for
This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.
Which of these equations is the result of applying the backward Euler method to solve for 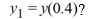
(Multiple Choice)
4.9/5  (33)
(33)
Consider the following initial value problem on the interval [0, 1]
![Consider the following initial value problem on the interval [0, 1] Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Y<sub>n</sub> values to start the fourth-order backward differentiation formula. Y<sub>1</sub> = 2.157777 Y<sub>2</sub>= 2.3322791 Y<sub>3</sub> = 2.5253944 Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places. Y<sub>5</sub> = ________](https://storage.examlex.com/TBW1042/11eeb833_703d_6b19_9020_e5b0e28017cd_TBW1042_11.jpg) Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y5 = ________
Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y5 = ________
(Short Answer)
4.7/5  (37)
(37)
Consider the initial value problem 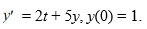 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
Which of these is the correct formula for
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
Which of these is the correct formula for 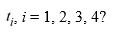
(Multiple Choice)
4.9/5  (38)
(38)
Consider the initial value problem 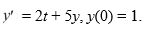 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
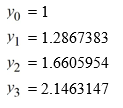 Which of the following show a portion of the formula for the corrected value of
Which of the following show a portion of the formula for the corrected value of 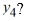
(Multiple Choice)
4.8/5  (38)
(38)
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 65.6 tanh(0.19t), t 3.0, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 3.10 seconds.Using a step size of h = 0.10 seconds, compute the vertical distance traveled in the first 3.10 seconds.
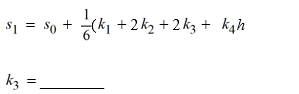
(Multiple Choice)
4.8/5  (37)
(37)
Consider the initial value problem
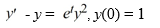 The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25.
The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25.
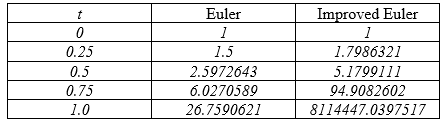 Based on the table above, which of the following is true regarding the given initial value problem?
Based on the table above, which of the following is true regarding the given initial value problem?
(Multiple Choice)
4.7/5  (40)
(40)
Consider the following initial value problem
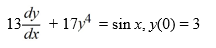 How would you need to rewrite this problem in order to apply Euler's method to approximate the solution of this problem at a value of x?
How would you need to rewrite this problem in order to apply Euler's method to approximate the solution of this problem at a value of x?
(Multiple Choice)
4.9/5  (47)
(47)
Showing 21 - 40 of 63
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)