Exam 2: First-Order Differential Equations
Exam 1: Introduction28 Questions
Exam 2: First-Order Differential Equations73 Questions
Exam 3: Second-Order Linear Differential Equations119 Questions
Exam 4: Higher-Order Linear Differential Equations54 Questions
Exam 5: Series Solutions of Second-Order Linear Equations81 Questions
Exam 6: The Laplace Transform57 Questions
Exam 7: Systems of First-Order Linear Equations97 Questions
Exam 8: Numerical Methods63 Questions
Exam 9: Nonlinear Differential Equations and Stability76 Questions
Exam 10: Partial Differential Equations and Fourier Series44 Questions
Exam 11: Boundary Value Problems and Sturm-Liouville Theory19 Questions
Select questions type
A pie is moved from the oven at 475 degrees Fahrenheit to a freezer at 25 degrees Fahrenheit. After 10 minutes, the pie has cooled to 425 degrees Fahrenheit.
Let T(t) be the temperature of the pie t minutes after it has been moved to the freezer. Formulate an initial-value problem whose solution is T(t).
(Essay)
4.9/5  (37)
(37)
Consider the differential equation 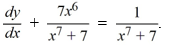 .What choice of the arbitrary constant in the general solution ensures that the solution curve passes through the point (1, 4)?
.What choice of the arbitrary constant in the general solution ensures that the solution curve passes through the point (1, 4)?
(Short Answer)
4.7/5  (29)
(29)
Which of the following is an accurate conclusion that can be made using the existence and uniqueness theorem for first-order nonlinear equations for this initial value problem?
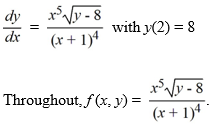
(Multiple Choice)
4.8/5  (45)
(45)
A city's water reservoir contains 7 billion cubic meters (bcm) of water. The purification system ensures that the concentration of pollutants remains constant at 0.5 kilograms per bcm, and sensors will trigger an alarm if the concentration of pollutants rises above 1 kilogram per bcm. Water flows in and out of the reservoir at the same rate of 0.20 bcm per day, and the concentration of pollutants in the inflow is 1.9 kilograms per bcm. At all times, the reservoir is well mixed.Set up a differential equation whose solution x(t) is the amount of pollutant in the reservoir at time t.
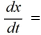 ________________
________________
(Short Answer)
4.9/5  (37)
(37)
Consider the differential equation 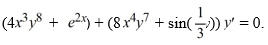 What is the general solution of this differential equation?
What is the general solution of this differential equation?
(Multiple Choice)
4.8/5  (41)
(41)
What is the two-parameter family of solutions of the second-order differential equation
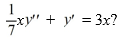
(Multiple Choice)
4.7/5  (29)
(29)
Consider the autonomous differential equation
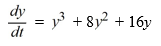 dentify the following statement as TRUE or FALSE:A solution curve passing through the point (0, -2) tends to 0 as t .
dentify the following statement as TRUE or FALSE:A solution curve passing through the point (0, -2) tends to 0 as t .
(True/False)
4.9/5  (31)
(31)
Consider the differential equation 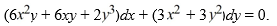 Find an integrating factor μ(x) so that the following differential equation is exact:
Find an integrating factor μ(x) so that the following differential equation is exact:
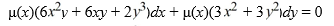
(Essay)
4.8/5  (36)
(36)
Identify the integrating factor for this linear differential equation: 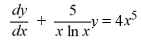
(Short Answer)
4.7/5  (44)
(44)
Find the general solution to the differential equation tan( 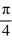 x)
x)
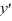 + y = -5 sin(
+ y = -5 sin( 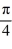 x).
x).
(Multiple Choice)
4.9/5  (41)
(41)
Which of the following statements are true for this initial-value problem? Select all that apply 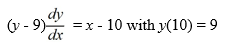
(Multiple Choice)
4.9/5  (34)
(34)
Consider the autonomous differential equation
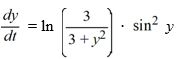 Which of the following statements is true?
Which of the following statements is true?
(Multiple Choice)
4.9/5  (36)
(36)
Which of the following is an accurate conclusion that can be made using the existence and uniqueness theorem for first-order differential equations for this initial value problem?
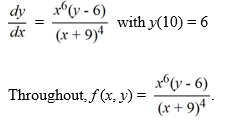
(Multiple Choice)
4.8/5  (43)
(43)
A ball is thrown from the top of a tall building with a speed of 12 meters per second. Suppose the ball hits the ground with a speed of 69 meters per second. (Recall that the acceleration due to gravity is 9.8 m/s2.)What is the time  (in seconds) of impact? Round your answer to the nearest hundredth of a second.
(in seconds) of impact? Round your answer to the nearest hundredth of a second.
(Short Answer)
4.8/5  (40)
(40)
Identify the integrating factor for this linear differential equation:
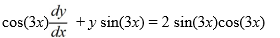
(Essay)
4.7/5  (39)
(39)
On another planet, a ball dropped from a height of 5 meters takes 3 seconds to hit the ground.
Let g be the acceleration due to gravity on this planet, v0 the initial velocity of the ball, and x0 the initial height of the ball above the ground. Write a formula for the height of the ball, x(t), above the ground at time t.
(Essay)
4.8/5  (37)
(37)
Find the general solution of the differential equation x 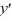 - 2y =
- 2y = 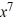 , x > 0.
, x > 0.
(Multiple Choice)
4.9/5  (33)
(33)
On another planet, a ball dropped from a height of 5 meters takes 4.5 seconds to hit the ground.Find the amount of time it takes the ball to hit the ground if it is dropped from a height of 122 meters. Round your answer to the nearest tenth of a second.
(Short Answer)
4.9/5  (40)
(40)
Showing 41 - 60 of 73
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)