Exam 8: Operational Amplifier Circuits, Filters, Oscillators and CMOS Digital Logic Circuits
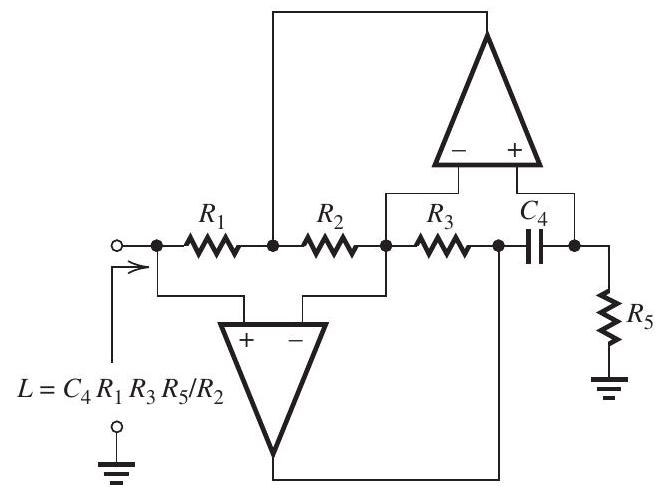 Figure 14.1.1
It is required to design a fifth-order Butterworth low-pass filter with a de gain of unity, a passband edge of , and a maximum deviation in the passband transmission of (i.e., ).
(a) Find the transfer function and give and of each of the two pairs of complex-conjugate poles. Also, specify the frequency of the real pole.
(b) Provide a complete circuit realization of the filter as a cascade of two second-order sections and a first-order section. For the second-order sections, use realizations based on the inductancesimulation circuit of Fig. 14.1.1. For the first-order section, use an op amp-RC circuit. Design so that all capacitors are equal to and as many of the resistors as possible are equal. Give the complete circuit and specify the values of all resistors.
(c) What is the attenuation achieved at the stopband edge, ?
Figure 14.1.1
It is required to design a fifth-order Butterworth low-pass filter with a de gain of unity, a passband edge of , and a maximum deviation in the passband transmission of (i.e., ).
(a) Find the transfer function and give and of each of the two pairs of complex-conjugate poles. Also, specify the frequency of the real pole.
(b) Provide a complete circuit realization of the filter as a cascade of two second-order sections and a first-order section. For the second-order sections, use realizations based on the inductancesimulation circuit of Fig. 14.1.1. For the first-order section, use an op amp-RC circuit. Design so that all capacitors are equal to and as many of the resistors as possible are equal. Give the complete circuit and specify the values of all resistors.
(c) What is the attenuation achieved at the stopband edge, ?
(a)
![(a) Figure 14.1.2 Figure 14.1.2 shows the s -plane locations of the poles. Here, \begin{aligned} \omega_{p} & \equiv \text { frequency of the passband edge }=10^{4} \mathrm{rad} / \mathrm{s} \\ \epsilon & \equiv \text { passband ripple factor }=1 \end{aligned} The pair of complex-conjugate poles p_{1} and p_{1}^{*} have \omega_{01}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and \begin{aligned} \frac{\omega_{01}}{2 Q_{1}} & =\omega_{01} \cos 72^{\circ} \\ \Rightarrow Q_{1} & =\frac{1}{2 \cos 72^{\circ}}=1.618 \end{aligned} The pair of complex-conjugate poles p_{2} and p_{2}^{*} have \omega_{02}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and Q_{2}=\frac{1}{2 \cos 36^{\circ}}=0.618 The real pole p_{3} has a frequency \omega_{03}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} Thus, the transfer function of the fifth-order lowpass filter is T(s)=\frac{10^{20}}{\left(s+10^{4}\right)\left(s^{2}+s \frac{10^{4}}{1.618}+10^{8}\right)\left(s^{2}+s \frac{10^{4}}{0.618}+10^{8}\right)} where the numerator was found by enforcing the condition T(0)=1 (b) Refer to Figure 14.1.3 Figure 14.1.3 Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here, \begin{aligned} C & =10 \mathrm{nF} \\ \omega_{0} & =10^{4}=\frac{1}{C R} \\ R & =\frac{1}{\omega_{0} C}=\frac{1}{10^{4} \times 10 \times 10^{-9}} \\ & =10 \mathrm{k} \Omega \end{aligned} For the circuit realizing \left(p_{1}, p_{1}^{*}\right) , Q R=1.618 \times 10=16.18 \mathrm{k} \Omega For the circuit realizing \left(p_{2}, p_{2}^{*}\right) , Q R=0.618 \times 10=6.18 \mathrm{k} \Omega Each circuit has a unity de gain. Figure 14.1.4 Figure 14.1.4 shows the circuit for realizing the real-axis pole, p_{3} . Here C=10 \mathrm{nF} \quad \text { and } \quad R=\frac{1}{\omega_{0} C}=10 \mathrm{k} \Omega The feedback resistance is selected equal to R so as to obtain a unity de gain. Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5 (c) \begin{aligned} |T| & =\frac{1}{\sqrt{1+\left(\omega / \omega_{p}\right)^{2 N}}} \\ A & =10 \log \left[1+\left(\omega / \omega_{p}\right)^{2 N}\right], \mathrm{dB} \end{aligned} where \omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} \quad \text { and } \quad N=5 At \omega=\omega_{S}=2 \times 10^{4} \mathrm{rad} / \mathrm{s} , \begin{aligned} A & =10 \log \left(1+2^{10}\right) \\ & =30.1 \mathrm{~dB} \end{aligned} Figure 14.1.6](https://storage.examlex.com/TBO1243/11eeb9e9_cbc6_6811_9342_d50370e2831b_TBO1243_00.jpg)
Figure 14.1.2
Figure 14.1.2 shows the -plane locations of the poles. Here,
The pair of complex-conjugate poles and have
and
The pair of complex-conjugate poles and have
and
The real pole has a frequency
Thus, the transfer function of the fifth-order lowpass filter is
where the numerator was found by enforcing the condition
(b) Refer to Figure 14.1.3
![(a) Figure 14.1.2 Figure 14.1.2 shows the s -plane locations of the poles. Here, \begin{aligned} \omega_{p} & \equiv \text { frequency of the passband edge }=10^{4} \mathrm{rad} / \mathrm{s} \\ \epsilon & \equiv \text { passband ripple factor }=1 \end{aligned} The pair of complex-conjugate poles p_{1} and p_{1}^{*} have \omega_{01}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and \begin{aligned} \frac{\omega_{01}}{2 Q_{1}} & =\omega_{01} \cos 72^{\circ} \\ \Rightarrow Q_{1} & =\frac{1}{2 \cos 72^{\circ}}=1.618 \end{aligned} The pair of complex-conjugate poles p_{2} and p_{2}^{*} have \omega_{02}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and Q_{2}=\frac{1}{2 \cos 36^{\circ}}=0.618 The real pole p_{3} has a frequency \omega_{03}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} Thus, the transfer function of the fifth-order lowpass filter is T(s)=\frac{10^{20}}{\left(s+10^{4}\right)\left(s^{2}+s \frac{10^{4}}{1.618}+10^{8}\right)\left(s^{2}+s \frac{10^{4}}{0.618}+10^{8}\right)} where the numerator was found by enforcing the condition T(0)=1 (b) Refer to Figure 14.1.3 Figure 14.1.3 Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here, \begin{aligned} C & =10 \mathrm{nF} \\ \omega_{0} & =10^{4}=\frac{1}{C R} \\ R & =\frac{1}{\omega_{0} C}=\frac{1}{10^{4} \times 10 \times 10^{-9}} \\ & =10 \mathrm{k} \Omega \end{aligned} For the circuit realizing \left(p_{1}, p_{1}^{*}\right) , Q R=1.618 \times 10=16.18 \mathrm{k} \Omega For the circuit realizing \left(p_{2}, p_{2}^{*}\right) , Q R=0.618 \times 10=6.18 \mathrm{k} \Omega Each circuit has a unity de gain. Figure 14.1.4 Figure 14.1.4 shows the circuit for realizing the real-axis pole, p_{3} . Here C=10 \mathrm{nF} \quad \text { and } \quad R=\frac{1}{\omega_{0} C}=10 \mathrm{k} \Omega The feedback resistance is selected equal to R so as to obtain a unity de gain. Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5 (c) \begin{aligned} |T| & =\frac{1}{\sqrt{1+\left(\omega / \omega_{p}\right)^{2 N}}} \\ A & =10 \log \left[1+\left(\omega / \omega_{p}\right)^{2 N}\right], \mathrm{dB} \end{aligned} where \omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} \quad \text { and } \quad N=5 At \omega=\omega_{S}=2 \times 10^{4} \mathrm{rad} / \mathrm{s} , \begin{aligned} A & =10 \log \left(1+2^{10}\right) \\ & =30.1 \mathrm{~dB} \end{aligned} Figure 14.1.6](https://storage.examlex.com/TBO1243/11eeb9e9_cbc6_6812_9342_27033439ab5c_TBO1243_00.jpg)
Figure 14.1.3
Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here,
For the circuit realizing ,
For the circuit realizing ,
Each circuit has a unity de gain.
![(a) Figure 14.1.2 Figure 14.1.2 shows the s -plane locations of the poles. Here, \begin{aligned} \omega_{p} & \equiv \text { frequency of the passband edge }=10^{4} \mathrm{rad} / \mathrm{s} \\ \epsilon & \equiv \text { passband ripple factor }=1 \end{aligned} The pair of complex-conjugate poles p_{1} and p_{1}^{*} have \omega_{01}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and \begin{aligned} \frac{\omega_{01}}{2 Q_{1}} & =\omega_{01} \cos 72^{\circ} \\ \Rightarrow Q_{1} & =\frac{1}{2 \cos 72^{\circ}}=1.618 \end{aligned} The pair of complex-conjugate poles p_{2} and p_{2}^{*} have \omega_{02}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and Q_{2}=\frac{1}{2 \cos 36^{\circ}}=0.618 The real pole p_{3} has a frequency \omega_{03}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} Thus, the transfer function of the fifth-order lowpass filter is T(s)=\frac{10^{20}}{\left(s+10^{4}\right)\left(s^{2}+s \frac{10^{4}}{1.618}+10^{8}\right)\left(s^{2}+s \frac{10^{4}}{0.618}+10^{8}\right)} where the numerator was found by enforcing the condition T(0)=1 (b) Refer to Figure 14.1.3 Figure 14.1.3 Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here, \begin{aligned} C & =10 \mathrm{nF} \\ \omega_{0} & =10^{4}=\frac{1}{C R} \\ R & =\frac{1}{\omega_{0} C}=\frac{1}{10^{4} \times 10 \times 10^{-9}} \\ & =10 \mathrm{k} \Omega \end{aligned} For the circuit realizing \left(p_{1}, p_{1}^{*}\right) , Q R=1.618 \times 10=16.18 \mathrm{k} \Omega For the circuit realizing \left(p_{2}, p_{2}^{*}\right) , Q R=0.618 \times 10=6.18 \mathrm{k} \Omega Each circuit has a unity de gain. Figure 14.1.4 Figure 14.1.4 shows the circuit for realizing the real-axis pole, p_{3} . Here C=10 \mathrm{nF} \quad \text { and } \quad R=\frac{1}{\omega_{0} C}=10 \mathrm{k} \Omega The feedback resistance is selected equal to R so as to obtain a unity de gain. Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5 (c) \begin{aligned} |T| & =\frac{1}{\sqrt{1+\left(\omega / \omega_{p}\right)^{2 N}}} \\ A & =10 \log \left[1+\left(\omega / \omega_{p}\right)^{2 N}\right], \mathrm{dB} \end{aligned} where \omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} \quad \text { and } \quad N=5 At \omega=\omega_{S}=2 \times 10^{4} \mathrm{rad} / \mathrm{s} , \begin{aligned} A & =10 \log \left(1+2^{10}\right) \\ & =30.1 \mathrm{~dB} \end{aligned} Figure 14.1.6](https://storage.examlex.com/TBO1243/11eeb9e9_cbc6_6813_9342_3be08edb07aa_TBO1243_00.jpg)
Figure 14.1.4
Figure 14.1.4 shows the circuit for realizing the real-axis pole, . Here
The feedback resistance is selected equal to so as to obtain a unity de gain.
Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5
![(a) Figure 14.1.2 Figure 14.1.2 shows the s -plane locations of the poles. Here, \begin{aligned} \omega_{p} & \equiv \text { frequency of the passband edge }=10^{4} \mathrm{rad} / \mathrm{s} \\ \epsilon & \equiv \text { passband ripple factor }=1 \end{aligned} The pair of complex-conjugate poles p_{1} and p_{1}^{*} have \omega_{01}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and \begin{aligned} \frac{\omega_{01}}{2 Q_{1}} & =\omega_{01} \cos 72^{\circ} \\ \Rightarrow Q_{1} & =\frac{1}{2 \cos 72^{\circ}}=1.618 \end{aligned} The pair of complex-conjugate poles p_{2} and p_{2}^{*} have \omega_{02}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and Q_{2}=\frac{1}{2 \cos 36^{\circ}}=0.618 The real pole p_{3} has a frequency \omega_{03}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} Thus, the transfer function of the fifth-order lowpass filter is T(s)=\frac{10^{20}}{\left(s+10^{4}\right)\left(s^{2}+s \frac{10^{4}}{1.618}+10^{8}\right)\left(s^{2}+s \frac{10^{4}}{0.618}+10^{8}\right)} where the numerator was found by enforcing the condition T(0)=1 (b) Refer to Figure 14.1.3 Figure 14.1.3 Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here, \begin{aligned} C & =10 \mathrm{nF} \\ \omega_{0} & =10^{4}=\frac{1}{C R} \\ R & =\frac{1}{\omega_{0} C}=\frac{1}{10^{4} \times 10 \times 10^{-9}} \\ & =10 \mathrm{k} \Omega \end{aligned} For the circuit realizing \left(p_{1}, p_{1}^{*}\right) , Q R=1.618 \times 10=16.18 \mathrm{k} \Omega For the circuit realizing \left(p_{2}, p_{2}^{*}\right) , Q R=0.618 \times 10=6.18 \mathrm{k} \Omega Each circuit has a unity de gain. Figure 14.1.4 Figure 14.1.4 shows the circuit for realizing the real-axis pole, p_{3} . Here C=10 \mathrm{nF} \quad \text { and } \quad R=\frac{1}{\omega_{0} C}=10 \mathrm{k} \Omega The feedback resistance is selected equal to R so as to obtain a unity de gain. Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5 (c) \begin{aligned} |T| & =\frac{1}{\sqrt{1+\left(\omega / \omega_{p}\right)^{2 N}}} \\ A & =10 \log \left[1+\left(\omega / \omega_{p}\right)^{2 N}\right], \mathrm{dB} \end{aligned} where \omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} \quad \text { and } \quad N=5 At \omega=\omega_{S}=2 \times 10^{4} \mathrm{rad} / \mathrm{s} , \begin{aligned} A & =10 \log \left(1+2^{10}\right) \\ & =30.1 \mathrm{~dB} \end{aligned} Figure 14.1.6](https://storage.examlex.com/TBO1243/11eeb9e9_cbc6_6814_9342_e51f64f8fc7d_TBO1243_00.jpg)
(c)
where
At ,
![(a) Figure 14.1.2 Figure 14.1.2 shows the s -plane locations of the poles. Here, \begin{aligned} \omega_{p} & \equiv \text { frequency of the passband edge }=10^{4} \mathrm{rad} / \mathrm{s} \\ \epsilon & \equiv \text { passband ripple factor }=1 \end{aligned} The pair of complex-conjugate poles p_{1} and p_{1}^{*} have \omega_{01}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and \begin{aligned} \frac{\omega_{01}}{2 Q_{1}} & =\omega_{01} \cos 72^{\circ} \\ \Rightarrow Q_{1} & =\frac{1}{2 \cos 72^{\circ}}=1.618 \end{aligned} The pair of complex-conjugate poles p_{2} and p_{2}^{*} have \omega_{02}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} and Q_{2}=\frac{1}{2 \cos 36^{\circ}}=0.618 The real pole p_{3} has a frequency \omega_{03}=\omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} Thus, the transfer function of the fifth-order lowpass filter is T(s)=\frac{10^{20}}{\left(s+10^{4}\right)\left(s^{2}+s \frac{10^{4}}{1.618}+10^{8}\right)\left(s^{2}+s \frac{10^{4}}{0.618}+10^{8}\right)} where the numerator was found by enforcing the condition T(0)=1 (b) Refer to Figure 14.1.3 Figure 14.1.3 Each of the pair of complex-conjugate poles will be realized utilizing the low-pass circuit shown in Fig. 14.1.3. Here, \begin{aligned} C & =10 \mathrm{nF} \\ \omega_{0} & =10^{4}=\frac{1}{C R} \\ R & =\frac{1}{\omega_{0} C}=\frac{1}{10^{4} \times 10 \times 10^{-9}} \\ & =10 \mathrm{k} \Omega \end{aligned} For the circuit realizing \left(p_{1}, p_{1}^{*}\right) , Q R=1.618 \times 10=16.18 \mathrm{k} \Omega For the circuit realizing \left(p_{2}, p_{2}^{*}\right) , Q R=0.618 \times 10=6.18 \mathrm{k} \Omega Each circuit has a unity de gain. Figure 14.1.4 Figure 14.1.4 shows the circuit for realizing the real-axis pole, p_{3} . Here C=10 \mathrm{nF} \quad \text { and } \quad R=\frac{1}{\omega_{0} C}=10 \mathrm{k} \Omega The feedback resistance is selected equal to R so as to obtain a unity de gain. Placing the three sections in cascade provides the realization of the fifth-order Butterworth lowpass filter. The resulting circuit is shown in Fig. 14.1.5 (c) \begin{aligned} |T| & =\frac{1}{\sqrt{1+\left(\omega / \omega_{p}\right)^{2 N}}} \\ A & =10 \log \left[1+\left(\omega / \omega_{p}\right)^{2 N}\right], \mathrm{dB} \end{aligned} where \omega_{p}=10^{4} \mathrm{rad} / \mathrm{s} \quad \text { and } \quad N=5 At \omega=\omega_{S}=2 \times 10^{4} \mathrm{rad} / \mathrm{s} , \begin{aligned} A & =10 \log \left(1+2^{10}\right) \\ & =30.1 \mathrm{~dB} \end{aligned} Figure 14.1.6](https://storage.examlex.com/TBO1243/11eeb9e9_cbc6_6815_9342_2166bd2f8d44_TBO1243_00.jpg)
Figure 14.1.6
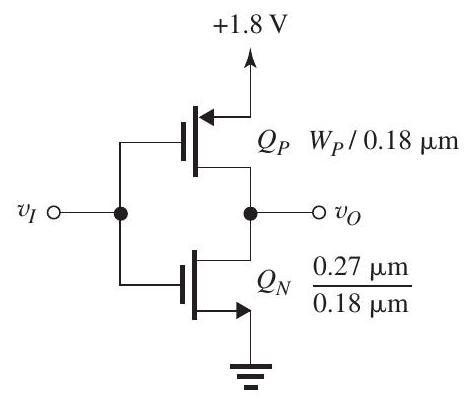 Figure 16.3.1
The CMOS inverter shown in Fig. 16.3.1 is fabricated in a technology having , , and .
(a) Find to obtain matched transistors.
(b) For , find the maximum load current that the inverter can sink while is not exceeding .
Figure 16.3.1
The CMOS inverter shown in Fig. 16.3.1 is fabricated in a technology having , , and .
(a) Find to obtain matched transistors.
(b) For , find the maximum load current that the inverter can sink while is not exceeding .
![(a) For matching, \begin{aligned} k_{n} & =k_{p} \\ \mu_{n} C_{o x}\left(\frac{W}{L}\right)_{N} & =\mu_{p} C_{o x}\left(\frac{W}{L}\right)_{P} \\ \mu_{n} \times \frac{0.27}{0.18} & =\frac{1}{3} \mu_{n} \times \frac{W_{p}}{0.18} \\ \Rightarrow W_{p} & =3 \times 0.27=0.81 \mu \mathrm{m} \end{aligned} (b) For v_{I}=1.8 \mathrm{~V}, Q_{N} will be operating in the triode region: i_{D N}=k_{n}\left[\left(v_{G S}-V_{t n}\right) v_{D S}-\frac{1}{2} v_{D S}^{2}\right] For v_{O}=0.1 \mathrm{~V} , \begin{aligned} i_{D N} & =0.4 \times \frac{0.27}{0.18}\left[(1.8-0.4) \times 0.1-\frac{1}{2} \times 0.1^{2}\right] \\ & =0.081 \mathrm{~mA} \\ & =81 \mu \mathrm{A} \end{aligned}](https://storage.examlex.com/TBO1243/11eeb9e9_cbc8_8afe_9342_cd6413435010_TBO1243_00.jpg)
(a) For matching,
(b) For will be operating in the triode region:
For ,
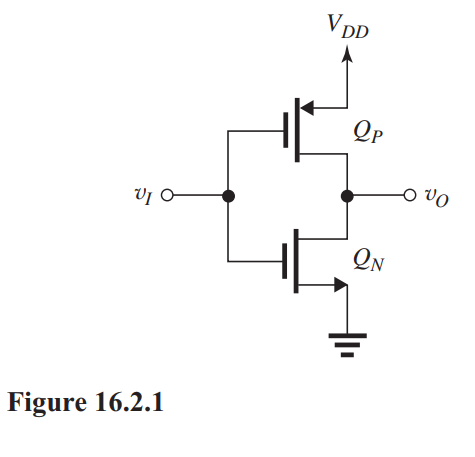 The CMOS inverter shown in Fig. 16.2.1 has and is fabricated in a process for which , and . For this problem, neglect the Early effect. Both and use the minimum channel length allowed. For .
(a) Find the dimensions that must have in order for the inverter switching to occur at .
(b) What are the noise margins of the inverter?
(c) What current flows in and at the switching point?
(d) For , what is the maximum current that can sink while is limited to ?
The CMOS inverter shown in Fig. 16.2.1 has and is fabricated in a process for which , and . For this problem, neglect the Early effect. Both and use the minimum channel length allowed. For .
(a) Find the dimensions that must have in order for the inverter switching to occur at .
(b) What are the noise margins of the inverter?
(c) What current flows in and at the switching point?
(d) For , what is the maximum current that can sink while is limited to ?
![Figure 16.2.1 (a) For the inverter switching to occur at 0.9 \mathrm{~V} , which is V_{D D} / 2, Q_{N} and Q_{P} must be matched: \begin{aligned} k_{n} & =k_{p} \\ \mu_{n} C_{O x}\left(\frac{W}{L}\right)_{N} & =\mu_{p} C_{O x}\left(\frac{W}{L}\right)_{P} \end{aligned} Thus, \frac{(W / P)_{P}}{(W / L)_{N}}=\frac{\mu_{n}}{\mu_{p}}=4 Since L_{N}=L_{P}=0.18 \mu \mathrm{m} and \begin{aligned} \left(\frac{W}{L}\right)_{N} & =1.5 \\ \Rightarrow W_{N} & =1.5 \times 0.18=0.27 \mu \mathrm{m} \\ W_{P} & =4 W_{N}=4 \times 0.27=1.08 \mu \mathrm{m} \end{aligned} we obtain \left(\frac{W}{L}\right)_{P}=\frac{1.08 \mu \mathrm{m}}{0.18 \mu \mathrm{m}} (b) \begin{aligned} V_{O H} & =V_{D D}=1.8 \mathrm{~V} \\ V_{O L} & =0 \mathrm{~V} \\ V_{I L} & =\frac{1}{8}\left(3 V_{D D}+2 V_{t}\right) \\ & =\frac{1}{8}(3 \times 1.8+2 \times 0.4) \\ & =0.775 \mathrm{~V} \\ N M_{L} & =V_{I L}-V_{O L}=0.775-0=0.775 \mathrm{~V} \\ N M_{H} & =N M_{L}=0.775 \mathrm{~V} \end{aligned} (c) At the switching point, Q_{N} and Q_{P} operate in saturation: \begin{aligned} I_{D} & =\frac{1}{2} \mu_{n} C_{o x}\left(\frac{W}{L}\right)_{N}\left(\frac{V_{D D}}{2}-V_{t}\right)^{2} \\ & =\frac{1}{2} \times 0.4 \times 1.5(0.9-0.4)^{2} \\ & =0.075 \mathrm{~mA}=75 \mu \mathrm{A} \end{aligned} (d) For v_{I}=1.8 \mathrm{~V}, Q_{N} is operating in the triode region: i_{D N}=k_{n}\left[\left(v_{G S}-V_{t n}\right) v_{D S}-\frac{1}{2} v_{D S}^{2}\right] For v_{G S}=1.8 \mathrm{~V} and v_{D S}=0.4 \mathrm{~V} , \begin{aligned} i_{D N} & =0.4 \times 1.5\left[(1.8-0.4) 0.4-\frac{1}{2} \times 0.4^{2}\right] \\ & =0.288 \mathrm{~mA} \end{aligned}](https://storage.examlex.com/TBO1243/11eeb9e9_cbc8_3cdc_9342_51e86455f9fa_TBO1243_00.jpg)
Figure 16.2.1
(a) For the inverter switching to occur at , which is and must be matched:
Thus,
Since and
we obtain
(b)
(c) At the switching point, and operate in saturation:
(d) For is operating in the triode region:
For and ,
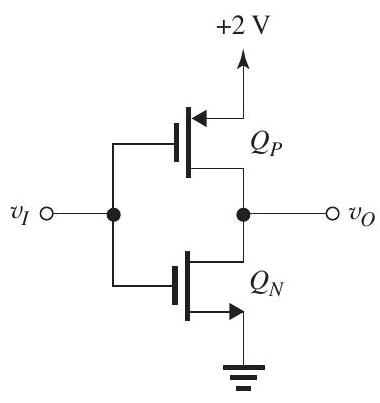 Figure 16.1.1
(a) For the CMOS inverter in Fig. 16.1.1, and have and . Sketch and clearly label the VTC versus and give values for the noise margins and . What is the output resistance when ?
(b) Provide the CMOS realization of the logic function.
Figure 16.1.1
(a) For the CMOS inverter in Fig. 16.1.1, and have and . Sketch and clearly label the VTC versus and give values for the noise margins and . What is the output resistance when ?
(b) Provide the CMOS realization of the logic function.
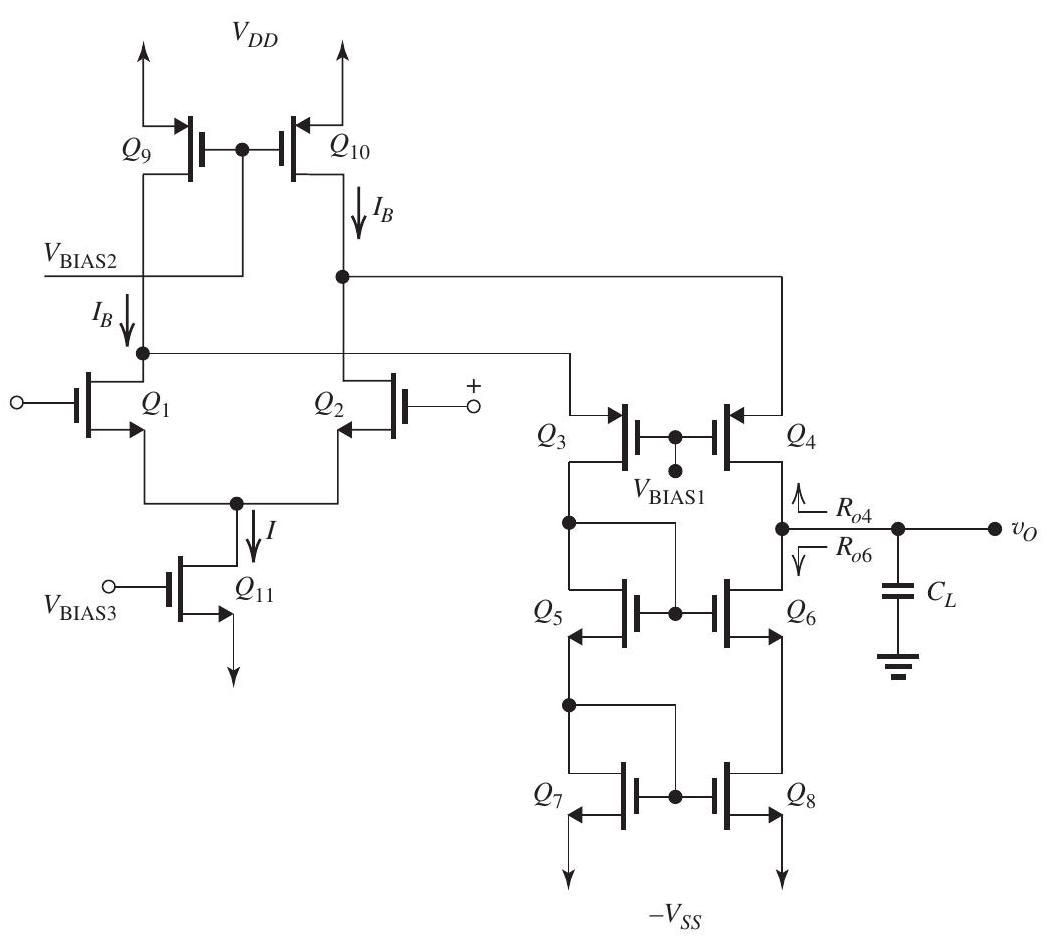 Figure 13.2.1
It is required to design the folded-cascode op amp shown in Fig. 13.2.1. Let and , and assume that for all transistors, . Design so that the power dissipated in the circuit (with no input signal applied) is , and so that each of and is operating at a current four times that at which each of and is operating. Also, design so that all transistors operate at .
(a) Show that the current drawn from each of the two power supplies is , and hence find and that result in the circuit operating at its specified power dissipation.
(b) Find the dc current at which each of to is operating. Present your results in a table.
(c) Find the input common-mode range.
(d) Find the required values of , and that result in the maximum allowable value of to be as high as possible.
(e) Find the allowable range of .
(f) Find the overall transconductance .
(g) Find the output resistance .
(h) Find the low-frequency voltage gain.
(i) If the amplifier at its output is modeled by a controlled current-source (where is the differential input voltage) feeding the output resistance and the total capacitance at the output node , find the value of that results in the amplifier having a unity-gain bandwidth of . Assume that the dominant pole is that formed at the output.
Figure 13.2.1
It is required to design the folded-cascode op amp shown in Fig. 13.2.1. Let and , and assume that for all transistors, . Design so that the power dissipated in the circuit (with no input signal applied) is , and so that each of and is operating at a current four times that at which each of and is operating. Also, design so that all transistors operate at .
(a) Show that the current drawn from each of the two power supplies is , and hence find and that result in the circuit operating at its specified power dissipation.
(b) Find the dc current at which each of to is operating. Present your results in a table.
(c) Find the input common-mode range.
(d) Find the required values of , and that result in the maximum allowable value of to be as high as possible.
(e) Find the allowable range of .
(f) Find the overall transconductance .
(g) Find the output resistance .
(h) Find the low-frequency voltage gain.
(i) If the amplifier at its output is modeled by a controlled current-source (where is the differential input voltage) feeding the output resistance and the total capacitance at the output node , find the value of that results in the amplifier having a unity-gain bandwidth of . Assume that the dominant pole is that formed at the output.
In the cross-coupled oscillator circuit shown in Fig. 15.1.1, represents the loss of each inductor. Each transistor is operating at a transconductance and has an output resistance . Find the oscillation frequency and explain why the circuit oscillates at this frequency. Also, derive an expression for the minimum value of needed to obtain sustained oscillations.
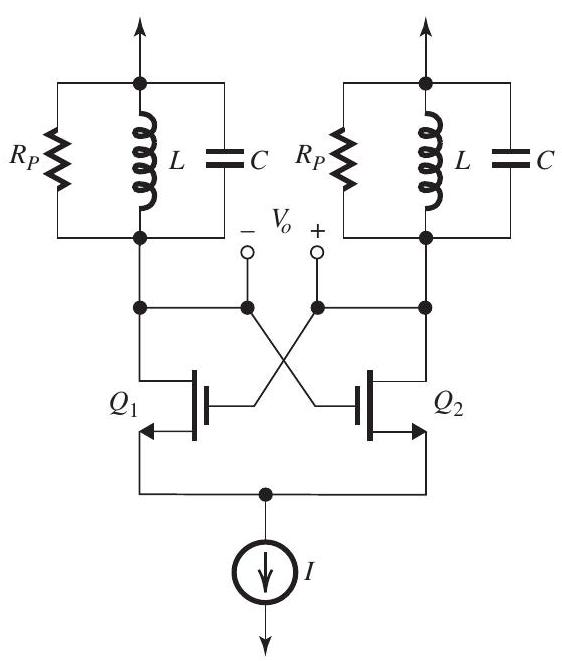 Figure 15.1.1
Figure 15.1.1
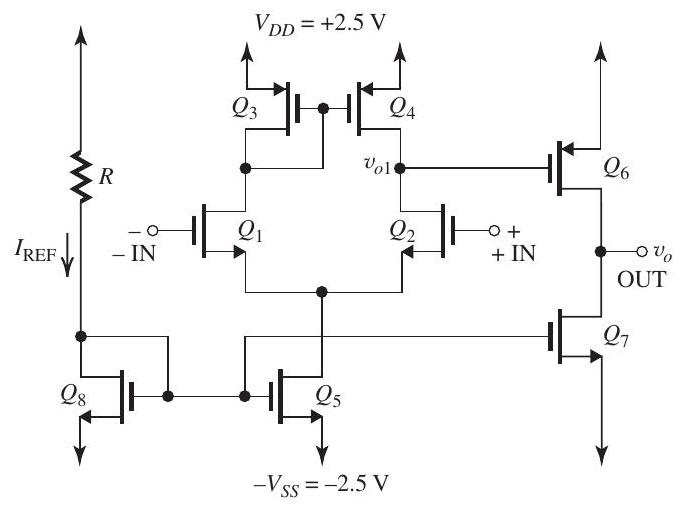 Figure 13.1.1
For the two-stage CMOS op amp shown in Fig. 13.1.1, all transistors have the same channel length , and . Transistors , and are matched; and are matched; and and are matched.
Parts (a) to (d) below deal with de bias calculations, and in these, assume the two input terminals are grounded and neglect the Early effect.
(a) Find the values of , and so that a dc voltage of appears at the gate of and dc current of flows in the drains of and .
(b) Find and that will result in each of and operating with an overdrive voltage of .
(c) Find and that will result in a dc voltage of at the gates of and .
(d) What de voltage appears at the gate of ? Find that will result in zero de current flowing through the output terminal of the amplifier.
(e) Find the input common-mode range.
(f) Find the allowable range of the output signal swing.
(g) Find the values of , and .
(h) Find the value of the differential gain of the first stage, .
(i) Recalling that the common-mode gain of the current-mirror-loaded differential amplifier is given by , where is the output resistance of , find , the commonmode gain, and the CMRR in .
(j) Find , and .
(k) Find the voltage gain of the second stage, .
(1) Find the overall differential voltage gain and the output resistance .
(m) If the feedback loop around the amplifier is closed by connecting the output terminal to the inverting input terminal, find the closedloop gain (between the non-inverting input terminal and the output) specified to four significant digits and determine the closed-loop output resistance .
(n) If, alternatively, the feedback loop around the op amp is closed by connecting the feedback network shown in Fig. 13.1.2, find the new values of and and the values of , the closed-loop gain , and the output resistance .
Figure 13.1.1
For the two-stage CMOS op amp shown in Fig. 13.1.1, all transistors have the same channel length , and . Transistors , and are matched; and are matched; and and are matched.
Parts (a) to (d) below deal with de bias calculations, and in these, assume the two input terminals are grounded and neglect the Early effect.
(a) Find the values of , and so that a dc voltage of appears at the gate of and dc current of flows in the drains of and .
(b) Find and that will result in each of and operating with an overdrive voltage of .
(c) Find and that will result in a dc voltage of at the gates of and .
(d) What de voltage appears at the gate of ? Find that will result in zero de current flowing through the output terminal of the amplifier.
(e) Find the input common-mode range.
(f) Find the allowable range of the output signal swing.
(g) Find the values of , and .
(h) Find the value of the differential gain of the first stage, .
(i) Recalling that the common-mode gain of the current-mirror-loaded differential amplifier is given by , where is the output resistance of , find , the commonmode gain, and the CMRR in .
(j) Find , and .
(k) Find the voltage gain of the second stage, .
(1) Find the overall differential voltage gain and the output resistance .
(m) If the feedback loop around the amplifier is closed by connecting the output terminal to the inverting input terminal, find the closedloop gain (between the non-inverting input terminal and the output) specified to four significant digits and determine the closed-loop output resistance .
(n) If, alternatively, the feedback loop around the op amp is closed by connecting the feedback network shown in Fig. 13.1.2, find the new values of and and the values of , the closed-loop gain , and the output resistance .
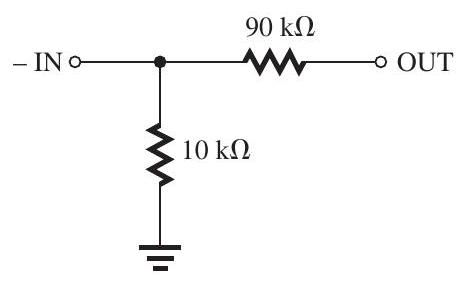 Figure 13.1.2
Figure 13.1.2
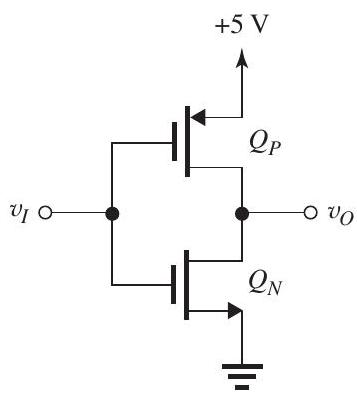 Figure 16.4.1
The transistors in the CMOS inverter in Fig. 16.4.1 have , and .
(a) What is the value of the gate threshold?
(b) For , what is the resistance between the output terminal and the supply? If a resistance is connected between the output terminal and ground, what will be?
Figure 16.4.1
The transistors in the CMOS inverter in Fig. 16.4.1 have , and .
(a) What is the value of the gate threshold?
(b) For , what is the resistance between the output terminal and the supply? If a resistance is connected between the output terminal and ground, what will be?
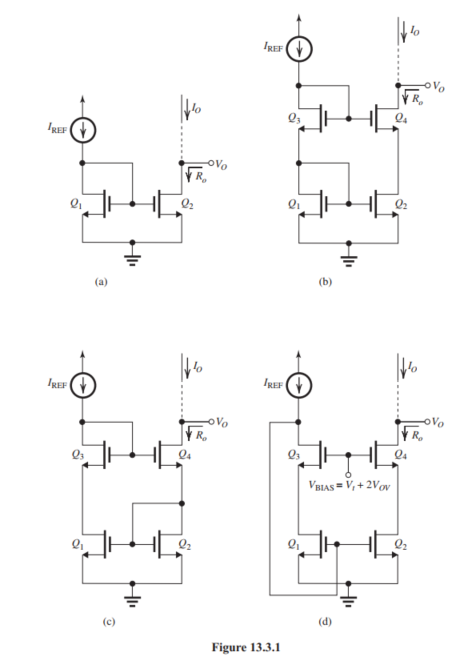 In the current-mirror circuits in Fig. 13.3.1, all transistors are operating at the same current and have the same and the same . Identify each current-mirror (i.e., give its name) and give its output resistance in terms of , and . Also, give the minimum voltage each mirror requires to operate properly. Give in terms of and .
In the current-mirror circuits in Fig. 13.3.1, all transistors are operating at the same current and have the same and the same . Identify each current-mirror (i.e., give its name) and give its output resistance in terms of , and . Also, give the minimum voltage each mirror requires to operate properly. Give in terms of and .
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)