Exam 9: Quadratic Equations, Inequalities, and Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
Tell what restrictions, if any, must be made on , and (all real numbers) to guarantee that is a real number. Assume that the denominator is not zero.
(Short Answer)
4.8/5  (28)
(28)
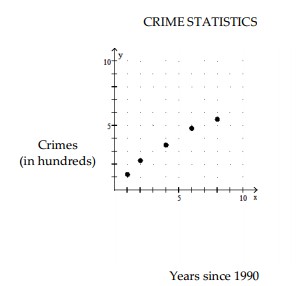
Determine whether a linear or quadratic function would be a more appropriate model for the graphed data. If linear, tell whether the slope should be positive or negative. If quadratic, decide whether the coefficient a of should be positive or negative.
-
(Multiple Choice)
4.9/5  (36)
(36)
If the trinomial is a perfect square, what can we conclude about the equation
(Multiple Choice)
4.9/5  (37)
(37)
Choose the one alternative that best completes the statement or answers the question.
Identify which graph matches the equation.
-
(Multiple Choice)
4.8/5  (29)
(29)
Choose the one alternative that best completes the statement or answers the question.
Use the quadratic formula to solve the equation. (All solutions are real numbers.)
-
(Multiple Choice)
4.8/5  (42)
(42)
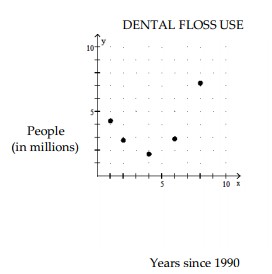
Determine whether a linear or quadratic function would be a more appropriate model for the graphed data. If linear, tell whether the slope should be positive or negative. If quadratic, decide whether the coefficient a of should be positive or negative.
-
(Multiple Choice)
4.8/5  (35)
(35)
Use the discriminant to determine if the equation can be solved by factoring. If the equation can be solved by factoring, then factor it.
-
(Multiple Choice)
4.9/5  (29)
(29)
Solve the problem, if possible. Round your answer to the nearest tenth, when appropriate.
-A parking lot measures by . A sidewalk of uniform width is to completely surround the lot. If the sidewalk can cover , how wide will the sidewalk be?
(Multiple Choice)
5.0/5  (32)
(32)
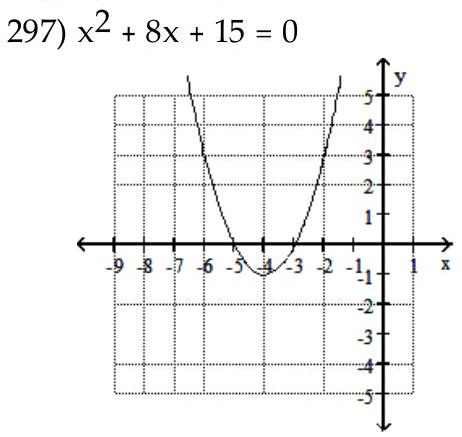
Use the graph of a quadratic function to find the solution set of the equation or inequality.
-
(Multiple Choice)
4.9/5  (37)
(37)
Showing 321 - 339 of 339
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)