Exam 7: The Single-Sample Z Test
Exam 1: Science and Statistics17 Questions
Exam 2: Organizing Data, Variables and Measurement13 Questions
Exam 3: Measures of Central Tendency16 Questions
Exam 4: Measures of Variation23 Questions
Exam 5: Standard Scores Z Scores12 Questions
Exam 6: Probability, Hypothesis Testing and Inferential Statistics12 Questions
Exam 7: The Single-Sample Z Test10 Questions
Exam 8: The Single-Sample T Test15 Questions
Exam 9: The T Test for Independent Groups Samples32 Questions
Exam 11: Comparing More Than Two Groups19 Questions
Exam 12: One-Way Between-Subjects Analysis of Variance Anova21 Questions
Exam 13: One-Way Repeated Measures Anova16 Questions
Exam 14: Using Designs With More Than One Independent Variable and Two-Way Between-Subjects Anova13 Questions
Exam 15: Correlational Research and Correlation Coefficients22 Questions
Exam 16: Advanced Correlational Techniques: Regression Analysis9 Questions
Exam 17: Chi-Square Tests21 Questions
Exam 18: Tests for Ordinal Data19 Questions
Select questions type
A researcher is interested in whether students who are musicians have higher intelligence test scores than students in the general population. The researcher predicts that playing a musical instrument is associated with higher intelligence test scores. The researcher selects a sample of 75 musicians from local high schools and gives them an intelligence test. She compares their average intelligence to that of students in the general population and finds that zobt = +1.92. This is a _____ test and the researcher should conclude _____.
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
A
Explain why 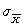 decreases as the size of the samples in the sampling distribution increases. Your answer should include an explanation based on the formula for
decreases as the size of the samples in the sampling distribution increases. Your answer should include an explanation based on the formula for 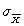 and an explanation of why this formula makes sense (in other words, why would increasing the size of each sample in the sampling distribution cause
and an explanation of why this formula makes sense (in other words, why would increasing the size of each sample in the sampling distribution cause 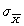 to decrease?).
to decrease?).
Free
(Essay)
4.7/5  (29)
(29)
Correct Answer:
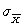 decreases when the sample size increases first because the formula for
decreases when the sample size increases first because the formula for 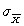 is to divide by the square root of N. Thus, as N increases, we are dividing by a larger number, resulting in a smaller number. This makes sense because as sample size increases, the mean of each sample should be closer to (we are including more of the population in the samples, and thus the sample means would be more similar to ), and thus the standard deviation (or the standard error of the mean) would be smaller because the sample means on which it is calculated would be closer to , resulting in less variability.
is to divide by the square root of N. Thus, as N increases, we are dividing by a larger number, resulting in a smaller number. This makes sense because as sample size increases, the mean of each sample should be closer to (we are including more of the population in the samples, and thus the sample means would be more similar to ), and thus the standard deviation (or the standard error of the mean) would be smaller because the sample means on which it is calculated would be closer to , resulting in less variability.
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-Calculate the 95% confidence interval for the population mean based on the sample mean.
Free
(Short Answer)
4.8/5  (41)
(41)
Correct Answer:
100.11-106.89
Given: For one section of the SAT: = 500 and = 100. The SAT was given to a sample of N = 35 and the mean SAT for this sample was 536. Calculate the z test for this sample mean. Does this sample differ significantly from the population for a two-tailed test?
(Essay)
4.8/5  (30)
(30)
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-What are H0 and Ha for this study?
(Short Answer)
4.8/5  (42)
(42)
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-Compute Zobt.
(Short Answer)
4.8/5  (36)
(36)
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-Is this a one- or two-tailed test?
(Short Answer)
4.9/5  (31)
(31)
Which of the following might one do in order to increase the power of a z test?
(Multiple Choice)
4.7/5  (42)
(42)
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-Should H0 be rejected? What should the researcher conclude?
(Short Answer)
4.8/5  (32)
(32)
A researcher is interested in whether students who attend private elementary schools do better or worse on a standard test of intelligence than the general population of elementary school children. A random sample of 75 students at a private elementary school is tested and has a mean intelligence test score of 103.5. The average for the general population of elementary school children is 100 ( = 15).
-What is zcv?
(Short Answer)
4.8/5  (37)
(37)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)