Exam 5: Network Models
Exam 1: Introduction to Modeling30 Questions
Exam 2: Introduction to Spreadsheet Modeling30 Questions
Exam 3: Introduction to Optimization Modeling30 Questions
Exam 4: Linear Programming Models31 Questions
Exam 5: Network Models30 Questions
Exam 6: Optimization Models With Integer Variables30 Questions
Exam 7: Nonlinear Optimization Models30 Questions
Exam 8: Evolutionary Solver: An Alternative Optimization Procedure30 Questions
Exam 9: Decision Making Under Uncertainty30 Questions
Exam 10: Introduction to Simulation Modeling30 Questions
Exam 11: Simulation Models30 Questions
Exam 12: Queueing Models30 Questions
Exam 13: Regression and Forecasting Models30 Questions
Exam 14: Data Mining30 Questions
Select questions type
In transportation problems,the three sets of input numbers that are required are capacities,demands and flows.
(True/False)
4.9/5  (31)
(31)
Exhibit 5-3
Steve the auto parts salesman is trying to navigate his way between the rural west Texas towns of Jonestown and Upland. The possible routes for this trip are shown below, along with the mileage along each route.
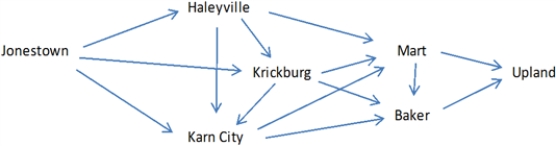 Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3.Suppose the roads leading into and out of Krickburg are unpaved,so Steve would only be able to travel half of his usual 60 mile/hour speed on those routes.Modify the model to account for this condition.Would the shortest path change from the base case solution
Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3.Suppose the roads leading into and out of Krickburg are unpaved,so Steve would only be able to travel half of his usual 60 mile/hour speed on those routes.Modify the model to account for this condition.Would the shortest path change from the base case solution
(Essay)
4.7/5  (32)
(32)
Exhibit 5-1
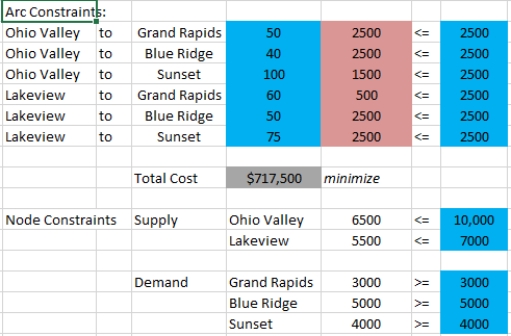
Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which can produce up to 10,000 tons per month and the Lakeview plant which can produce up to 7,000 tons per month. Sinclair sells its polyethylene to three different auto manufacturing plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below:
Grand Rapids Blue Ridge Sunset Ohio Valley 50 40 100 Lakeview 60 50 75
-Refer to Exhibit 5-1.Formulate (write out algebraically)an LP transportation model to help Sinclair minimize its shipping costs.
(Essay)
4.9/5  (28)
(28)
For all routes with positive flows in an optimized transportation problem,the reduced cost will be:
(Multiple Choice)
4.7/5  (41)
(41)
The cost of an arc in a shortest path problem is not necessarily equal to the distance of the arc.
(True/False)
4.9/5  (27)
(27)
Exhibit 5-3
Steve the auto parts salesman is trying to navigate his way between the rural west Texas towns of Jonestown and Upland. The possible routes for this trip are shown below, along with the mileage along each route.
 Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3.Implement the appropriate model in Solver and determine the shortest path for Steve.How many total miles will he travel on his trip
Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3.Implement the appropriate model in Solver and determine the shortest path for Steve.How many total miles will he travel on his trip
(Essay)
4.9/5  (32)
(32)
Exhibit 5-2
A small engineering firm employs one civil engineer, two engineering technicians, and one summer intern. The types of projects the firm does includes surveys (typically 7 per month), designs (5 per month), and construction project plans (four per month). The times, in hours, required for each employee to complete teach type of project are shown below. Based on their capabilities and time spent on travel and administrative tasks, the engineer, tech 1, tech 2, and intern can handle 5, 4, 4, and 3 projects per month, respectively.
 -Refer to Exhibit 5-2.Suppose Tech 2 will not be available during the next month.Keeping the same number of design and construction plan projects,how many survey projects would the firm be able to do
What would be the revised assignment plan in that case
-Refer to Exhibit 5-2.Suppose Tech 2 will not be available during the next month.Keeping the same number of design and construction plan projects,how many survey projects would the firm be able to do
What would be the revised assignment plan in that case
(Essay)
4.7/5  (36)
(36)
The graphical representation of a network in an optimization problem can be an aid in the development of a spreadsheet model.
(True/False)
4.8/5  (37)
(37)
Exhibit 5-2
A small engineering firm employs one civil engineer, two engineering technicians, and one summer intern. The types of projects the firm does includes surveys (typically 7 per month), designs (5 per month), and construction project plans (four per month). The times, in hours, required for each employee to complete teach type of project are shown below. Based on their capabilities and time spent on travel and administrative tasks, the engineer, tech 1, tech 2, and intern can handle 5, 4, 4, and 3 projects per month, respectively.
 -Refer to Exhibit 5-2.Implement a LP model in Solver and determine the optimal monthly assignment plan for the firm.What is the total number of hours that will be assigned to projects each month
-Refer to Exhibit 5-2.Implement a LP model in Solver and determine the optimal monthly assignment plan for the firm.What is the total number of hours that will be assigned to projects each month
(Essay)
4.8/5  (35)
(35)
Exhibit 5-1
Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which can produce up to 10,000 tons per month and the Lakeview plant which can produce up to 7,000 tons per month. Sinclair sells its polyethylene to three different auto manufacturing plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below:
Grand Rapids Blue Ridge Sunset Ohio Valley 50 40 100 Lakeview 60 50 75
-Refer to Exhibit 5-1.Suppose the shipping capacity between any two plants was limited to 2500 tons per month.Design and implement a network flow version of this model in Solver and obtain the optimal shipping plan.How much more would the shipping plan cost Sinclair in that case
(Essay)
4.7/5  (39)
(39)
Showing 21 - 30 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)