Exam 2: Introduction to Optimization and Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis51 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet89 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling73 Questions
Exam 6: Integer Linear Programming73 Questions
Exam 7: Goal Programming and Multiple Objective Optimization62 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis77 Questions
Exam 10: Discriminant Analysis60 Questions
Exam 11: Time Series Forecasting116 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory80 Questions
Exam 14: Decision Analysis101 Questions
Exam 15: Project Management Online63 Questions
Select questions type
The Happy Pet pet food company produces dog and cat food. Each food is comprised of meat, soybeans and fillers. The company earns a profit on each product but there is a limited demand for them. The pounds of ingredients required and available, profits and demand are summarized in the following table. The company wants to plan their product mix, in terms of the number of bags produced, in order to maximize profit.
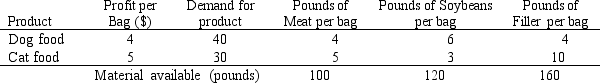 a.Formulate the LP model for this problem.
b.Solve the problem using the graphical method.
a.Formulate the LP model for this problem.
b.Solve the problem using the graphical method.
(Essay)
4.8/5  (37)
(37)
Jones Furniture Company produces beds and desks for college students. The production process requires carpentry and varnishing. Each bed requires 6 hours of carpentry and 4 hour of varnishing. Each desk requires 4 hours of carpentry and 8 hours of varnishing. There are 36 hours of carpentry time and 40 hours of varnishing time available. Beds generate $30 of profit and desks generate $40 of profit. Demand for desks is limited so at most 8 will be produced.
a.Formulate the LP model for this problem.
b.Solve the problem using the graphical method.
(Essay)
4.9/5  (29)
(29)
Solve the following LP problem graphically using level curves.
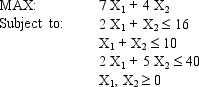
(Short Answer)
4.9/5  (36)
(36)
The objective function for a LP model is 3 X1 + 2 X2. If X1 = 20 and X2 = 30, what is the value of the objective function?
(Multiple Choice)
4.8/5  (26)
(26)
The constraint for resource 1 is 5 X1 + 4 X2 200. If X1 = 40 and X2 = 20, how many additional units, if any, of resource 1 are employed above the minimum of 200?
(Multiple Choice)
4.8/5  (34)
(34)
Solve the following LP problem graphically by enumerating the corner points.
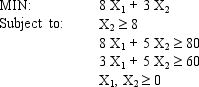
(Short Answer)
4.9/5  (38)
(38)
Jim's winery blends fine wines for local restaurants. One of his customers has requested a special blend of two burgundy wines, call them A and B. The customer wants 500 gallons of wine and it must contain at least 100 gallons of A and be at least 45% B. The customer also specified that the wine have an alcohol content of at least 12%. Wine A contains 14% alcohol while wine B contains 10%. The blend is sold for $10 per gallon. Wine A costs $4 per gallon and B costs $3 per gallon. The company wants to determine the blend that will meet the customer's requirements and maximize profit.
a.Formulate the LP model for this problem.
b.Solve the problem using the graphical method.
c.How much profit will Jim make on the order?
(Essay)
4.9/5  (30)
(30)
If constraints are added to an LP model the feasible solution space will generally
(Multiple Choice)
4.9/5  (32)
(32)
The Big Bang explosives company produces customized blasting compounds for use in the mining industry. The two ingredients for these explosives are agent A and agent B. Big Bang just received an order for 1400 pounds of explosive. Agent A costs $5 per pound and agent B costs $6 per pound. The customer's mixture must contain at least 20% agent A and at least 50% agent B. The company wants to provide the least expensive mixture which will satisfy the customers requirements.
a.Formulate the LP model for this problem.
b.Solve the problem using the graphical method.
(Essay)
4.8/5  (28)
(28)
A company makes two products, X1 and X2. They require at least 20 of each be produced. Which set of lower bound constraints reflect this requirement?
(Multiple Choice)
4.8/5  (36)
(36)
The first step in formulating a linear programming problem is
(Multiple Choice)
4.7/5  (39)
(39)
The third step in formulating a linear programming problem is
(Multiple Choice)
4.9/5  (42)
(42)
Solve the following LP problem graphically by enumerating the corner points.
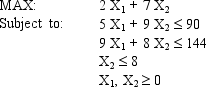
(Short Answer)
4.8/5  (37)
(37)
Joey Koons runs a small custom computer parts company. As a sideline he offers customized and pre-built computer system packages. In preparation for the upcoming school year, he has decided to offer two custom computer packages tailored for what he believes are current student needs. System A provides a strong computing capability at a reasonable cost while System B provides a much more powerful computing capability, but at a higher cost. Joey has a fairly robust parts inventory but is concerned about his stock of those components that are common to each proposed system. A portion of his inventory, the item cost, and inventory level is provided in the table below.
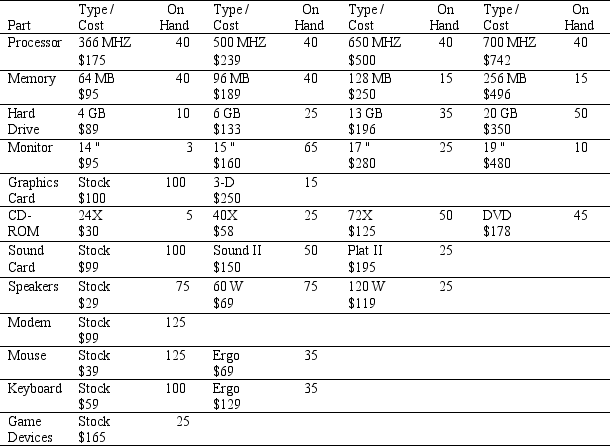 The requirements for each system are provided in the following table:
The requirements for each system are provided in the following table:
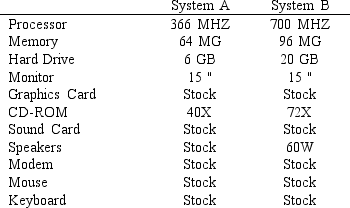 Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.
Each system requires assembly, testing and packaging. The requirements per system built and resources available are summarized in the table below.
 Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.
Formulate an LP for Dave's problem. Solve the model using the graphical method. What is Dave's preferred product mix? What profit does Dave expect to make from this product mix?
Joey is uncertain about product demand. In the past he has put together similar types of computer packages but his sales results vary. As a result is unwilling to commit all his in-house labor force to building the computer packages. He is confident he can sell all he can build and is not overly concerned with lost sales due to stock-outs. Based on his market survey, he has completed his advertising flyer and will offer System A for $ 1250 and will offer system B for $ 2325. Joey now needs to let his workers know how many of each system to build and he wants that mix to maximize his profits.
Formulate an LP for Dave's problem. Solve the model using the graphical method. What is Dave's preferred product mix? What profit does Dave expect to make from this product mix?
(Essay)
4.9/5  (43)
(43)
Solve the following LP problem graphically using level curves.
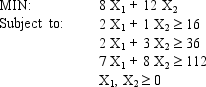
(Short Answer)
5.0/5  (36)
(36)
Solve the following LP problem graphically using level curves.
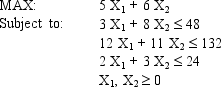
(Short Answer)
4.8/5  (36)
(36)
Showing 21 - 40 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)