Exam 2: Economists View of Behavior
Exam 1: Introduction29 Questions
Exam 2: Economists View of Behavior43 Questions
Exam 3: Markets, Organizations, and the Role of Knowledge43 Questions
Exam 4: Demand31 Questions
Exam 5: Production and Cost36 Questions
Exam 6: Market Structure47 Questions
Exam 7: Pricing With Market Power40 Questions
Exam 8: Economics of Strategy: Creating and Capturing Value41 Questions
Exam 9: Economics of Strategy: Game Theory32 Questions
Exam 10: Incentive Conflicts and Contracts39 Questions
Exam 11: Organizational Architecture39 Questions
Exam 12: Decision Rights: The Level of Empowerment37 Questions
Exam 13: Decision Rights: Bundling Tasks Into Jobs and Subunits36 Questions
Exam 14: Attracting and Retaining Qualified Employees44 Questions
Exam 15: Incentive Compensation38 Questions
Exam 16: Individual Performance Evaluation39 Questions
Exam 17: Divisional Performance Evaluation36 Questions
Exam 18: Corporate Governance39 Questions
Exam 19: Vertical Integration and Outsourcing43 Questions
Exam 20: Leadership: Motivating Change Within Organizations41 Questions
Exam 21: Understanding the Business Environment: The Economics of Regulation40 Questions
Exam 22: Ethics and Organizational Architecture38 Questions
Exam 23: Organizational Architecture and the Process of Management Innovation32 Questions
Select questions type
You have $64 to spend on fish (F) and chips (C). Suppose the price per unit of fish (Pf) is $8 and the price of chips (Pc) is $2. Your utility function for fish and chips is given asC. How many units of C and F should you buy to exhaust all income and maximize utility?
First note that to maximize utility, you have to be at equilibrium. This means, the following condition has to be satisfied:
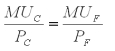 It is better to write this as:
It is better to write this as:
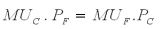 Now substitute the corresponding entities in the above expression:
Now substitute the corresponding entities in the above expression:
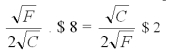 Cancelling the 2s in the denominator and cross-multiplying we get
C = 4 F
Now the second aspect of this is your income which is $64, which has to be spent on F and C. So your budget constraint should satisfy this condition:
64 = C Pc + F Pf or
64 = C 2 + 8 F and now from the previous condition we have
64 = (4 F) 2 + 8 F or
F = 4 units
C = 16 units and total utility is
Cancelling the 2s in the denominator and cross-multiplying we get
C = 4 F
Now the second aspect of this is your income which is $64, which has to be spent on F and C. So your budget constraint should satisfy this condition:
64 = C Pc + F Pf or
64 = C 2 + 8 F and now from the previous condition we have
64 = (4 F) 2 + 8 F or
F = 4 units
C = 16 units and total utility is
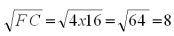
(Essay)
4.8/5  (42)
(42)
Robinson pays $100 for tickets to see his favorite sports team play. With 10 minutes left in the game, his team is losing heavily and has no chance of winning the game. Robinson chooses to stay until the end of game because he wants to get the full value for his admission price. As an economist, you should advise Robinson to:
(Multiple Choice)
4.9/5  (35)
(35)
Assume the quantity of apples is measured on the horizontal axis and the quantity of oranges is measured on the vertical axis. If the budget line rotates upward, while keeping the same horizontal intercept, then:
(Multiple Choice)
4.8/5  (41)
(41)
Ali inherits $10,000 from his great-great aunt in 2008. His great-great aunt's will requires that Ali spend the money before December 31, 2009. He can spend the money on two consumption goods: consumption in 2008 or consumption in 2009. This is Ali's only source of money. The interest rate on loans or savings is ten percent.
(a) How much could Ali spend in 2008 if he only consumes in 2008? How much could Ali spend in 2005 if he only consumes in 2009?
(b) What is the opportunity cost of consuming $1.00 in 2008, in terms of forgone consumption in 2009? Draw Ali's budget constraint and optimal consumption bundle. Please put 2008 consumption on the x-axis.
(c) Ali decides to spend 6000 dollars on consumption in 2008 and 4400 dollars. Show this optimal consumption bundle using a budget constraint and indifference curve diagram.
(Essay)
4.8/5  (38)
(38)
Assume that the quantity of CDs is measured on the horizontal axis, while the quantity of movie tickets is measured on the vertical axis. If available income decreases, then the new budget line:
(Multiple Choice)
5.0/5  (35)
(35)
Assume the quantity of apples is measured on the horizontal axis and the quantity of oranges is measured on the vertical axis. If Andy likes both apples and oranges, then his Marginal Rate of Substitution (i.e. the slope of an indifference curve) along the indifference curve indicates:
(Multiple Choice)
4.8/5  (36)
(36)
Assume Joseph spends his entire income on X and Y, and his indifference curves have the usual convex shape. If Joseph maximizes his utility, then:
(Multiple Choice)
4.7/5  (41)
(41)
What is the relationship between the slope of the budget line to the notion of opportunity cost?
(Essay)
4.9/5  (40)
(40)
Suppose that canned soup is inferior. This means that when:
(Multiple Choice)
4.8/5  (35)
(35)
Jim Range has to choose between buying more soda or more pasta for the week. He has a fixed income and he knows the prices of both products. Using indifference curves and budget constraint lines, illustrate the amount of soda and pasta that Jim will purchase. When he gets to the store, he finds the price of soda has fallen dramatically. How does this change his optimal purchase? Can a general rule of human behavior be developed from this graphical example?
(Essay)
4.9/5  (36)
(36)
Contrast the "Good Citizen Model" with the "Economic Model" to explain the reason why people engage in charitable behavior.
(Essay)
4.9/5  (36)
(36)
The demand for normal goods obeys the law of demand because of:
(Multiple Choice)
4.8/5  (34)
(34)
You purchase both potatoes and gasoline regularly. Your income increases, and you purchase more gasoline. This means that:
(Multiple Choice)
4.9/5  (42)
(42)
Assume MACROSOFT is planning to develop and sell a new word processor. It estimates that R&D expenses will amount to $300,000 for this new software, while it will have to invest an additional $150,000 to advertise and distribute the new product. If MACROSOFT's managers are risk-neutral, they will undertake this project if the expected revenues from the sales of the new software are:
(Multiple Choice)
4.8/5  (34)
(34)
Robert only consumes X and Y, and his indifference curves have the usual convex shape. Consider the consumption bundles (3, 9), (6, 6), and (9, 3) (hint: they lie on a straight line). If Robert is indifferent between (3, 9) and (9, 3), then:
(Multiple Choice)
4.8/5  (34)
(34)
What does the tangency between an indifference curve and the budget line determine?
(Essay)
4.8/5  (26)
(26)
It is commonly believed that the best ways to motivate an employee are (1) to improve the quality of the workplace and (2) to make the employee feel like he/she is part of the company. How would an economist analyze these statements?
(Essay)
4.8/5  (38)
(38)
Showing 21 - 40 of 43
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)