Exam 14: Oscillations
Exam 1: Representing Motion113 Questions
Exam 2: Motion in One Dimension174 Questions
Exam 3: Vectors and Motion in Two Dimensions183 Questions
Exam 4: Forces and Newtons Laws of Motion64 Questions
Exam 5: Applying Newtons Laws82 Questions
Exam 6: Gravity96 Questions
Exam 7: Rotational Motion95 Questions
Exam 8: Equilibrium Ad Elasticity73 Questions
Exam 9: Momentum103 Questions
Exam 10: Energy and Work223 Questions
Exam 11: Using Energy106 Questions
Exam 12: Thermal Properties of Matter220 Questions
Exam 13: Fluids115 Questions
Exam 14: Oscillations105 Questions
Exam 15: Traveling Waves and Sound94 Questions
Exam 16: Superposition and Standing Waves66 Questions
Exam 17: Wave Optics129 Questions
Exam 18: Ray Optics155 Questions
Exam 19: Optical Instruments137 Questions
Exam 20: Electric Fields and Forces95 Questions
Exam 21: Electric Potential144 Questions
Exam 22: Current and Resistance125 Questions
Exam 23: Circuits157 Questions
Exam 24: Magnetic Fields and Forces168 Questions
Exam 25: EM Induction and Em Waves185 Questions
Exam 26: AC Electricity122 Questions
Exam 27: Relativity126 Questions
Exam 28: Quantum Physics86 Questions
Exam 29: Atoms and Molecules105 Questions
Exam 30: Nuclear Physics175 Questions
Select questions type
A Christmas ornament made from a thin hollow glass sphere hangs from a small hook at its surface. It is observed to oscillate with a frequency of 2.50 Hz in a city where g = 9.80 m/s2. What is the radius of the ornament? The moment of inertia of a hollow sphere of mass M and radius R about a point on its edge is 5MR2/3.
(Multiple Choice)
4.8/5  (37)
(37)
A pendulum of length L is suspended from the ceiling of an elevator. When the elevator is at rest the period of the pendulum is T. How does the period of the pendulum change when the elevator moves upward with constant acceleration?
(Multiple Choice)
4.9/5  (38)
(38)
An object is attached to a vertical spring and bobs up and down between points A and B. Where is the object located when its kinetic energy is a maximum?
(Multiple Choice)
4.8/5  (41)
(41)
If the angular frequency of the motion of a simple harmonic oscillator is doubled, by what factor does the maximum acceleration of the oscillator change?
(Multiple Choice)
4.8/5  (29)
(29)
On the Moon, the acceleration of gravity is g/6. If a pendulum has a period T on Earth, what will its period be on the Moon?
(Multiple Choice)
4.7/5  (25)
(25)
If your heart is beating at 76.0 beats per minute, what is the frequency of your heart's oscillations in hertz?
(Multiple Choice)
4.7/5  (27)
(27)
A ball vibrates back and forth from the free end of an ideal spring having a force constant (spring constant) of 20 N/m. If the amplitude of this motion is 0.30 m, what is the kinetic energy of the ball when it is 0.30 m from its equilibrium position?
(Multiple Choice)
4.9/5  (39)
(39)
The position of an air-track cart that is oscillating on a spring is given by the equation x = (12.4 cm) cos[(6.35 s-1)t]. At what value of t after t = 0.00 s is the cart first located at x = 8.47 cm?
(Multiple Choice)
4.8/5  (40)
(40)
A spaceship captain lands on an unknown planet. Before venturing forth, he needs to find out the acceleration due to gravity on that planet. All he has available to him is some thin light string, a stopwatch, and a small 2.75-kg metal ball (it was a rough landing). So he lets the ball swing from a 1.5-m length of the string, starting at rest, and measures that it takes 1.9 s for it to swing from the place where he released it to the place where it first stops as it reverses direction. What is the acceleration due to gravity on this planet?
(Short Answer)
4.9/5  (37)
(37)
The position of an object that is oscillating on an ideal spring is given by x = (17.4 cm) cos[(5.46 s-1)t]. Write an expression for the acceleration of the particle as a function of time using the cosine function.
(Short Answer)
4.7/5  (32)
(32)
The figure shows a graph of the velocity v as a function of time t for a system undergoing simple harmonic motion. Which one of the following graphs represents the acceleration of this system as a function of time? 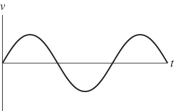 a)
a)
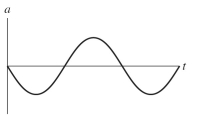 b)
b)
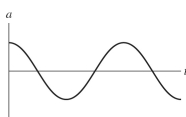 c)
c)
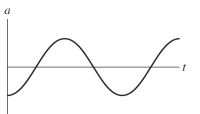 d)
d)
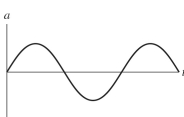
(Multiple Choice)
4.8/5  (40)
(40)
A simple pendulum having a bob of mass M has a period T. If you double M but change nothing else, what would be the new period?
(Multiple Choice)
4.7/5  (42)
(42)
When a certain simple pendulum is set swinging, its angular displacement θ as a function of time t obeys the equation θ = 8.5° cos(2.4 s-1t). How long is the pendulum?
(Short Answer)
4.8/5  (35)
(35)
A 3.42-kg stone hanging vertically from an ideal spring on the earth undergoes simple harmonic motion at a place where g = 9.80 m/s2. If the force constant (spring constant) of the spring is find the period of oscillation of this setup on a planet where g = 1.60 m/s2.
(Multiple Choice)
4.8/5  (36)
(36)
A guitar string is set into vibration with a frequency of 512 Hz. How many oscillations does it undergo each minute?
(Multiple Choice)
4.8/5  (40)
(40)
An air-track cart is attached to a spring and completes one oscillation every 5.67 s in simple harmonic motion. At time t = 0.00 s the cart is released at the position x = +0.250 m. What is the position of the cart when t = 29.6 s?
(Multiple Choice)
4.8/5  (34)
(34)
A ball is attached to an ideal spring and oscillates with a period T. If the mass of the ball is doubled, what is the new period?
(Multiple Choice)
4.9/5  (40)
(40)
A block attached to an ideal spring of force constant (spring constant) 15 N/m executes simple harmonic motion on a frictionless horizontal surface. At time t = 0 s, the block has a displacement of -0.90 m, a velocity of -0.80 m/s, and an acceleration of +2.9 m/s2 . The mass of the block is closest to
(Multiple Choice)
4.8/5  (30)
(30)
As shown in the figure, a 0.23-kg ball is suspended from a string 6.87 m long and is pulled slightly to the left. As the ball swings through the lowest part of its motion it encounters a spring attached to the wall. The spring pushes against the ball and eventually the ball is returned to its original starting position. Find the time for one complete cycle of this motion if the spring constant (force constant) is (Assume that once the pendulum ball hits the spring there is no effect due to the vertical movement of the ball.) 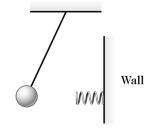
(Short Answer)
4.7/5  (36)
(36)
How much mass should be attached to a vertical ideal spring having a spring constant (force constant) of 39.5 N/m so that it will oscillate at 1.00 Hz?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 81 - 100 of 105
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)