Instruction 12.39 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. \[\begin{array} { | l | l | l | } \hline \text { Broker } & \text { Clients } & \text { Sles } \\ \hline 1 & 27 & 52 \\ \hline 2 & 11 & 37 \\ \hline 3 & 42 & 64 \\ \hline 4 & 33 & 55 \\ \hline 5 & 15 & 29 \\ \hline 6 & 15 & 34 \\ \hline 7 & 25 & 58 \\ \hline 8 & 36 & 59 \\ \hline 9 & 28 & 44 \\ \hline 10 & 30 & 48 \\ \hline 11 & 17 & 31 \\ \hline 12 & 22 & 38 \\ \hline \end{array}\] -Referring to Instruction 12.39,suppose the managers of the brokerage firm want to obtain a 99% prediction interval for the sales made by a broker who has brought into the firm 18 new customers.The prediction interval is from __________ to __________.

The answer of Instruction 12.39 The managers of a brokerage firm...

Instruction 12.29 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. \[\begin{array} { | l | l | l | } \hline \text { Broker } & \text { Clients } & \text { Sales } \\ \hline 1 & 27 & 52 \\ \hline 2 & 11 & 37 \\ \hline 3 & 42 & 64 \\ \hline 4 & 33 & 55 \\ \hline 5 & 15 & 29 \\ \hline 6 & 15 & 34 \\ \hline 7 & 25 & 58 \\ \hline 8 & 36 & 59 \\ \hline 9 & 28 & 44 \\ \hline 10 & 30 & 48 \\ \hline 11 & 17 & 31 \\ \hline 12 & 22 & 38 \\ \hline \end{array}\] -Referring to Instruction 12.29,the managers of the brokerage firm wanted to test the hypothesis that the number of new customers brought in had a positive impact on the amount of sales generated.At a level of significance of 0.01,the decision that should be made implies that the number of new customers brought in____________ (had or did not have)a positive impact on the amount of sales generated.

The answer of Instruction 12.29 The managers of a brokerage firm...

The sample correlation coefficient between X and Y is 0.375.It has been found out that the p-value is 0.256 when testing H0: ρ = 0 against the two-sided alternative H1: ρ ≠ 0.To test H0: ρ = 0 against the one-sided alternative H1: ρ < 0 at a significance level of 0.2,the p-value is

A) 0.256 / 2. B) (0.256)2. C) 1 - 0.256. D) 1 - 0.256 / 2. A) 0.256 / 2. B) (0.256)2. C) 1 - 0.256. D) 1 - 0.256 / 2.

Instruction 12.29 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. \[\begin{array} { | l | l | l | } \hline \text { Broker } & \text { Clients } & \text { Sales } \\ \hline 1 & 27 & 52 \\ \hline 2 & 11 & 37 \\ \hline 3 & 42 & 64 \\ \hline 4 & 33 & 55 \\ \hline 5 & 15 & 29 \\ \hline 6 & 15 & 34 \\ \hline 7 & 25 & 58 \\ \hline 8 & 36 & 59 \\ \hline 9 & 28 & 44 \\ \hline 10 & 30 & 48 \\ \hline 11 & 17 & 31 \\ \hline 12 & 22 & 38 \\ \hline \end{array}\] -Referring to Instruction 12.29,the managers of the brokerage firm wanted to test the hypothesis that the number of new customers brought in had a positive impact on the amount of sales generated.At a level of significance of 0.01,the null hypothesis should be ____________ (accepted or rejected).

The answer of Instruction 12.29 The managers of a brokerage firm...

Exam 12: Simple Linear Regression

Instruction 12.35 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: $\text { Regression statistics }$ MultipleR 0.8691 R Square 0.7554 Adjusted R Square 0.7467 Standard Error 44.4765 Observations 30.0000 $\text { ANOVA }$ df SS MS F Significance F Regression 1 171062.9193 171062.9193 86.4759 0.0000 Residual 28 55388.4309 1978.1582 Total 29 226451.3503 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept -95.0614 26.9183 -3.5315 0.0015 -150.2009 -39.9218 Download 3.7297 0.4011 9.2992 0.0000 2.9082 4.5513 $Instruction 12.35 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \text { Regression statistics } \begin{array}{|l|l|} \hline \text { MultipleR } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000\\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S S & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} -Referring to Instruction 12.35,what is the critical value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?$ $Instruction 12.35 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \text { Regression statistics } \begin{array}{|l|l|} \hline \text { MultipleR } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000\\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S S & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 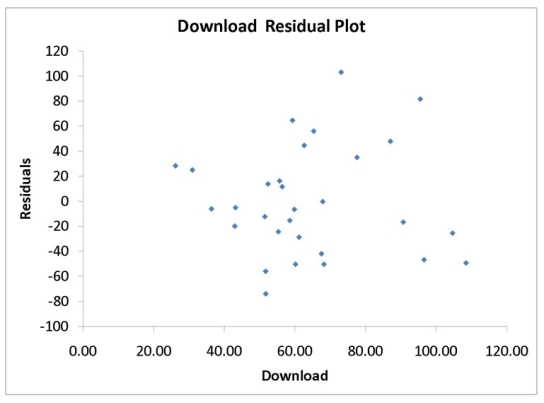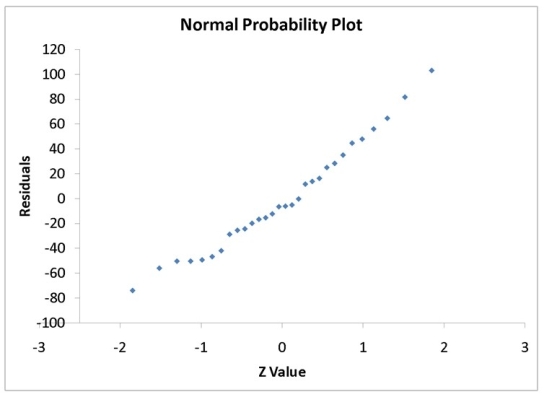\\ \hline \end{array} -Referring to Instruction 12.35,what is the critical value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?$ -Referring to Instruction 12.35,what is the critical value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?

(Short Answer)

4.8/5

(42)

Question 61

Instruction 12.12 The director of cooperative education at a university wants to examine the effect of cooperative education job experience on marketability in the workplace. She takes a random sample of four students. For these four, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student Coop jobs job Offer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Instruction 12.12,the coefficient of correlation is ____________.

(Short Answer)

4.9/5

(40)

Question 62

Instruction 12.2 A chocolate bar manufacturer is interested in trying to estimate how sales are influenced by the price of their product. To do this, the company randomly chooses six country towns and cities and offers the chocolate bar at different prices. Using chocolate bar sales as the dependent variable, the company will conduct a simple linear regression on the data below: $\begin{array} { | l | l | l | } \hline \text { City } & \text { Price(\$) } & \text { Syles } \\\hline \text { Toowoomba } & 1.30 & 100 \\\hline \text { Broken Hill } & 1.60 & 50 \\\hline \text { Bendigo } & 1.80 & 50 \\\hline \text { Kalgoorlie } & 2.00 & 40 \\\hline \text { Launceston } & 2.40 & 38 \\\hline \text { Port Augusta } & 2.50 & 32 \\\hline\end{array}$ -Referring to Instruction 12.2,what is the estimated slope parameter for the chocolate bar price and sales data?

(Multiple Choice)

4.8/5

(43)

Question 63

Instruction 12.39 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Clients Sles 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Instruction 12.39,suppose the managers of the brokerage firm want to obtain a 99% prediction interval for the sales made by a broker who has brought into the firm 18 new customers.The prediction interval is from to .

(Short Answer)

4.8/5

(33)

Question 64

Instruction 12.29 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Instruction 12.29,the managers of the brokerage firm wanted to test the hypothesis that the number of new customers brought in had a positive impact on the amount of sales generated.At a level of significance of 0.01,the decision that should be made implies that the number of new customers brought in____________ (had or did not have)a positive impact on the amount of sales generated.

(Short Answer)

4.9/5

(37)

Question 65

onfident that the mean amount of time needed to record one additional loan application is somewhere $\text { Regression statistics }$ MultipleR 0.9447 R Square 0.8924 Adjusted R Square 0.8886 Standard Error 0.3342 Observations 30 $\text { ANOVA }$ df S5 MS F Significance F Regression 1 25.9438 25.9438 232.2200 4.3946-15 Residual 28 3.1282 0.1117 Total 29 29.072 Coefficients Standard Error tStat p-value Lower 95\% Upper 95\% Intercept 0.4024 0.1236 3.2559 0.0030 0.1492 0.6555 Applications Recorded 0.0126 0.0008 15.2388 4.3946- 15 0.0109 0.0143 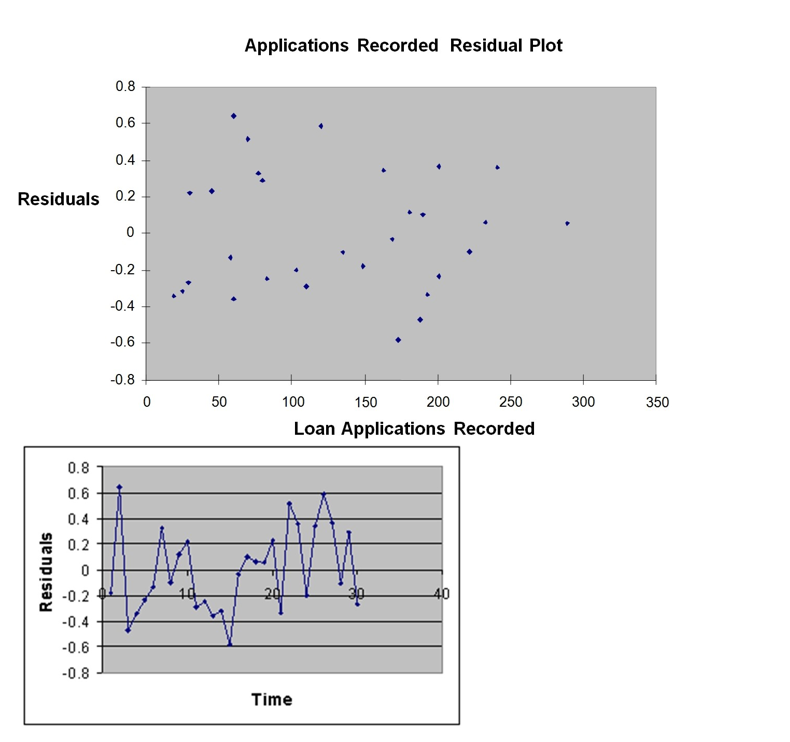$\text { Note: } 4.3946 \mathrm { E } - 15 \text { is } 4.3946 \times 10 ^ { - 15 } \text {. }$ $onfident that the mean amount of time needed to record one additional loan application is somewhere \text { Regression statistics } \begin{array}{|l|l|} \hline\text { MultipleR } & 0.9447 \\ \hline \text { R Square } & 0.8924 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.8886 \\ \hline \text { Standard Error } & 0.3342 \\ \hline \text { Observations } & 30 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S 5 & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \hline \text { Total } & 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \begin{array}{l} \text { Applications } \\ \text { Recorded } \end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l} 4.3946 \mathrm{E}- \\ 15 \end{array} & 0.0109 & 0.0143 \\ \hline \end{array} \text { Note: } 4.3946 \mathrm { E } - 15 \text { is } 4.3946 \times 10 ^ { - 15 } \text {. } -Referring to Instruction 12.36,the degrees of freedom for the F test on whether the number of loan applications recorded affects the amount of time are$ -Referring to Instruction 12.36,the degrees of freedom for the F test on whether the number of loan applications recorded affects the amount of time are

(Multiple Choice)

4.8/5

(40)

Question 66

If the correlation coefficient (r)= 1.00,then

(Multiple Choice)

4.7/5

(37)

Question 67

Instruction 12.38 The director of cooperative education at a university wants to examine the effect of cooperative education job experience on marketability in the workplace. She takes a random sample of four students. For these four, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student Coop Jobs Job Oifer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Instruction 12.38,suppose the director of cooperative education wants to obtain two 95% confidence interval estimates.One is for the mean number of job offers received by people who have had exactly one cooperative education job and one for people who have had two.The confidence interval for people who have had one cooperative education job would be the wider of the two intervals.

(True/False)

4.8/5

(43)

Question 68

The Durbin-Watson D statistic is used to check the assumption of normality.

(True/False)

4.8/5

(31)

Question 69

Instruction 12.11 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application. Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded. Below is the regression output: $\text { Regression statistics }$ MultipleR 0.9447 R Square 0.8924 Adjusted R Square 0.8886 Standard Error 0.3342 Observations 30 $\text { ANOVA }$ df S5 MS F Significance F Regression 1 25.9438 25.9438 232.2200 4.3946-15 Residual 28 3.1282 0.1117 Total 29 29.072 Coefficients Standard Error tStat p-value Lower 95\% Upper 95\% Intercept 0.4024 0.1236 3.2559 0.0030 0.1492 0.6555 Applications Recorded 0.0126 0.0008 15.2388 4.3946- 15 0.0109 0.0143 Note: 4.3946E-15 is 4.3946 × 10^-¹⁵. $Instruction 12.11 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application. Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded. Below is the regression output: \text { Regression statistics } \begin{array}{|l|l|} \hline\text { MultipleR } & 0.9447 \\ \hline \text { R Square } & 0.8924 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.8886 \\ \hline \text { Standard Error } & 0.3342 \\ \hline \text { Observations } & 30 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S 5 & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \hline \text { Total } & 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \begin{array}{l} \text { Applications } \\ \text { Recorded } \end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l} 4.3946 \mathrm{E}- \\ 15 \end{array} & 0.0109 & 0.0143 \\ \hline \end{array} Note: 4.3946E-15 is 4.3946 × 10-15. -Referring to Instruction 12.11,the estimated mean amount of time it takes to record one additional loan application is$ $Instruction 12.11 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application. Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded. Below is the regression output: \text { Regression statistics } \begin{array}{|l|l|} \hline\text { MultipleR } & 0.9447 \\ \hline \text { R Square } & 0.8924 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.8886 \\ \hline \text { Standard Error } & 0.3342 \\ \hline \text { Observations } & 30 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S 5 & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \hline \text { Total } & 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \begin{array}{l} \text { Applications } \\ \text { Recorded } \end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l} 4.3946 \mathrm{E}- \\ 15 \end{array} & 0.0109 & 0.0143 \\ \hline \end{array} Note: 4.3946E-15 is 4.3946 × 10-15. 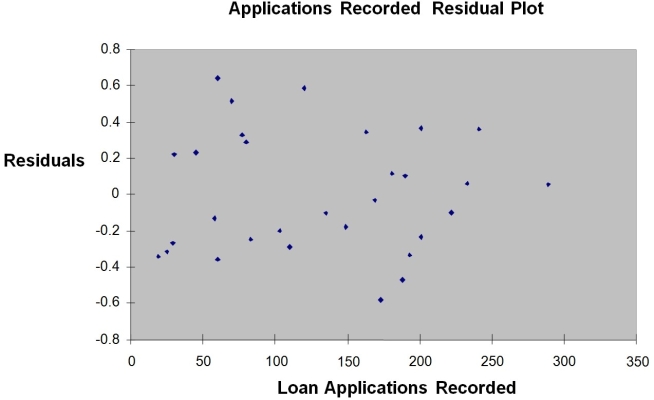-Referring to Instruction 12.11,the estimated mean amount of time it takes to record one additional loan application is$ -Referring to Instruction 12.11,the estimated mean amount of time it takes to record one additional loan application is

(Multiple Choice)

4.9/5

(28)

Question 70

The sample correlation coefficient between X and Y is 0.375.It has been found out that the p-value is 0.256 when testing H₀: ρ = 0 against the two-sided alternative H₁: ρ ≠ 0.To test H₀: ρ = 0 against the one-sided alternative H₁: ρ < 0 at a significance level of 0.2,the p-value is

(Multiple Choice)

4.9/5

(36)

Question 71

Instruction 12.4 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Instruction 12.4,set up a scatter diagram.

(Essay)

4.9/5

(34)

Question 72

Instruction 12.4 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Instruction 12.4,the least squares estimate of the Y-intercept is ____________.

(Short Answer)

4.9/5

(38)

Question 73

onfident that the mean amount of time needed to record one additional loan application is somewhere $\text { Regression statistics }$ MultipleR 0.9447 R Square 0.8924 Adjusted R Square 0.8886 Standard Error 0.3342 Observations 30 $\text { ANOVA }$ df S5 MS F Significance F Regression 1 25.9438 25.9438 232.2200 4.3946-15 Residual 28 3.1282 0.1117 Total 29 29.072 Coefficients Standard Error tStat p-value Lower 95\% Upper 95\% Intercept 0.4024 0.1236 3.2559 0.0030 0.1492 0.6555 Applications Recorded 0.0126 0.0008 15.2388 4.3946- 15 0.0109 0.0143 $\text { Note: } 4.3946 \mathrm { E } - 15 \text { is } 4.3946 \times 10 ^ { - 15 } \text {. }$ $onfident that the mean amount of time needed to record one additional loan application is somewhere \text { Regression statistics } \begin{array}{|l|l|} \hline\text { MultipleR } & 0.9447 \\ \hline \text { R Square } & 0.8924 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.8886 \\ \hline \text { Standard Error } & 0.3342 \\ \hline \text { Observations } & 30 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S 5 & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \hline \text { Total } & 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \begin{array}{l} \text { Applications } \\ \text { Recorded } \end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l} 4.3946 \mathrm{E}- \\ 15 \end{array} & 0.0109 & 0.0143 \\ \hline \end{array} \text { Note: } 4.3946 \mathrm { E } - 15 \text { is } 4.3946 \times 10 ^ { - 15 } \text {. } -Referring to Instruction 12.36,the p-value of the measured F test statistic to test whether the number of loan applications record affects the amount of time is$ -Referring to Instruction 12.36,the p-value of the measured F test statistic to test whether the number of loan applications record affects the amount of time is

(Multiple Choice)

4.9/5

(27)

Question 74

Instruction 12.29 The managers of a brokerage firm are interested in finding out if the number of new customers a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new customers they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Instruction 12.29,the managers of the brokerage firm wanted to test the hypothesis that the number of new customers brought in had a positive impact on the amount of sales generated.At a level of significance of 0.01,the null hypothesis should be ____________ (accepted or rejected).

(Short Answer)

4.9/5

(31)

Question 75

To avoid the pitfalls of regression,you should start with a scatter plot to observe the possible relationship between X and Y.

(True/False)

4.9/5

(30)

Question 76

Instruction 12.10 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: $\text { Regression statistics }$ MultipleR 0.8691 R Square 0.7554 Adjusted R Square 0.7467 Standard Error 44.4765 Observations 30.0000 $\text { ANOVA }$ df SS MS F Significance F Regression 1 171062.9193 171062.9193 86.4759 0.0000 Residual 28 55388.4309 1978.1582 Total 29 226451.3503 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept -95.0614 26.9183 -3.5315 0.0015 -150.2009 -39.9218 Download 3.7297 0.4011 9.2992 0.0000 2.9082 4.5513 $Instruction 12.10 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \text { Regression statistics } \begin{array}{|l|l|} \hline \text { MultipleR } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000\\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S S & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} -Referring to Instruction 12.10,which of the following is the correct interpretation for the slope coefficient?$ $Instruction 12.10 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \text { Regression statistics } \begin{array}{|l|l|} \hline \text { MultipleR } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \begin{array}{l} \text { Adjusted R } \\ \text { Square } \end{array} & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000\\ \hline \end{array} \text { ANOVA } \begin{array}{|l|l|l|l|l|l|} \hline & d f & S S & M S & F & \begin{array}{l} \text { Significance } \\ F \end{array} \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \\ \hline \end{array} \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { Coefficients } & \begin{array}{l} \text { Standard } \\ \text { Error } \end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} -Referring to Instruction 12.10,which of the following is the correct interpretation for the slope coefficient?$ -Referring to Instruction 12.10,which of the following is the correct interpretation for the slope coefficient?

(Multiple Choice)

4.8/5

(39)

Question 77

Instruction 12.27 The director of cooperative education at a university wants to examine the effect of cooperative education job experience on marketability in the workplace. She takes a random sample of four students. For these four, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student Coop jobs job Offer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Instruction 12.27,the director of cooperative education wanted to test the hypothesis that the true slope was equal to 3.0.The p-value of the test is between and .

(Essay)

4.7/5

(48)

Question 78

If you wanted to find out if alcohol consumptions (measured in ml)and grade point average on a four-point scale are linearly related,you would perform a

(Multiple Choice)

4.8/5

(32)

Question 79

Instruction 12.3 The director of cooperative education at a university wants to examine the effect of cooperative education job experience on marketability in the workplace. She takes a random sample of four students. For these four, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student Coop jobs job Offer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Instruction 12.3,the total sum of squares (SST)is ____________.

(Short Answer)

4.8/5

(36)

Question 80

Showing 61 - 80 of 207

If the correlation coefficient (r)= 1.00,then

The Durbin-Watson D statistic is used to check the assumption of normality.

The sample correlation coefficient between X and Y is 0.375.It has been found out that the p-value is 0.256 when testing H₀: ρ = 0 against the two-sided alternative H₁: ρ ≠ 0.To test H₀: ρ = 0 against the one-sided alternative H₁: ρ < 0 at a significance level of 0.2,the p-value is

To avoid the pitfalls of regression,you should start with a scatter plot to observe the possible relationship between X and Y.

If you wanted to find out if alcohol consumptions (measured in ml)and grade point average on a four-point scale are linearly related,you would perform a

Defining and Collecting Data

Organising and Visualising Data

Numerical Descriptive Measures

Basic Probability

Some Important Discrete Probability Distributions

The Normal Distribution and Other Continuous Distributions

Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Hypothesis Testing: Two-Sample Tests

Analysis of Variance

Introduction to Multiple Regression

Time-Series Forecasting and Index Numbers

Chi-Square Tests

Multiple Regression Model Building

Decision Making

Statistical Applications in Quality Management

Further Non-Parametric Tests

Filters