Exam 7: Introduction to Linear Programming
Exam 1: Introduction50 Questions
Exam 2: Introduction to Probability53 Questions
Exam 3: Probability Distributions52 Questions
Exam 4: Decision Analysis48 Questions
Exam 5: Utility and Game Theory49 Questions
Exam 6: Forecasting60 Questions
Exam 7: Introduction to Linear Programming54 Questions
Exam 8: Lp Sensitivity Analysis and Interpretation of Solution49 Questions
Exam 9: Linear Programming Applications42 Questions
Exam 10: Distribution and Network Problems57 Questions
Exam 11: Integer Linear Programming49 Questions
Exam 12: Advanced Optimization Application42 Questions
Exam 13: Project Scheduling: Pertcpm41 Questions
Exam 14: Inventory Models54 Questions
Exam 15: Waiting Line Models52 Questions
Exam 16: Simulation49 Questions
Exam 17: Markov Processes44 Questions
Select questions type
Consider the following linear program:
MAX 60X + 43Y
s.t.X + 3Y > 9
6X -0 2Y = 12
X + 2Y < 10
X,Y > 0
a.Write the problem in standard form.
b.What is the feasible region for the problem?
c.Show that regardless of the values of the actual objective function coefficients,the optimal solution will occur at one of two points.Solve for these points and then determine which one maximizes the current objective function.
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
a.MAX 60X + 43Y
S.T.X + 3Y - S1 = 9
6X - 2Y = 12
X + 2Y + S3 = 10
X,Y,S1,S3 > 0
b.Line segment of 6X - 2Y = 12 between (22/7,24/7)and (27/10,21/10).
c.Extreme points: (22/7,24/7)and (27/10,21/10).First one is optimal,giving Z = 336.
For the following linear programming problem,determine the optimal solution by the graphical solution method
Max -X + 2Y
s.t.6X - 2Y 3
-2X + 3Y - 6
X + Y 3
X,Y 0
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
X = 0.6 and Y = 2.4 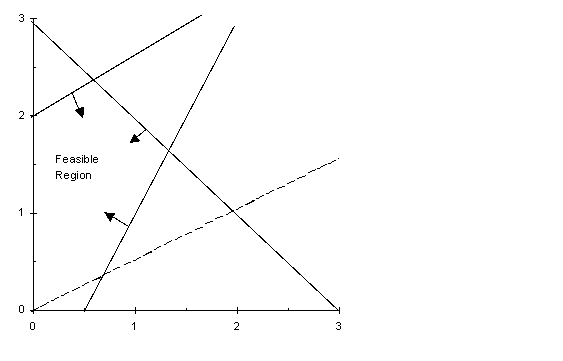
All of the following statements about a redundant constraint are correct EXCEPT
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
D
Solve the following linear program graphically.
MAX 5X + 7Y
s.t.X < 6
2X + 3Y < 19
X + Y < 8
X,Y > 0
(Essay)
4.9/5  (32)
(32)
As long as the slope of the objective function stays between the slopes of the binding constraints
(Multiple Choice)
4.8/5  (31)
(31)
A solution that satisfies all the constraints of a linear programming problem except the nonnegativity constraints is called
(Multiple Choice)
4.8/5  (32)
(32)
The improvement in the value of the objective function per unit increase in a right-hand side is the
(Multiple Choice)
4.9/5  (33)
(33)
Solve the following system of simultaneous equations.
6X + 2Y = 50
2X + 4Y = 20
(Essay)
4.9/5  (29)
(29)
Because surplus variables represent the amount by which the solution exceeds a minimum target,they are given positive coefficients in the objective function.
(True/False)
4.7/5  (34)
(34)
An unbounded feasible region might not result in an unbounded solution for a minimization or maximization problem.
(True/False)
4.8/5  (32)
(32)
A businessman is considering opening a small specialized trucking firm.To make the firm profitable,it is estimated that it must have a daily trucking capacity of at least 84,000 cu.ft.Two types of trucks are appropriate for the specialized operation.Their characteristics and costs are summarized in the table below.Note that truck 2 requires 3 drivers for long haul trips.There are 41 potential drivers available and there are facilities for at most 40 trucks.The businessman's objective is to minimize the total cost outlay for trucks.
 Solve the problem graphically and note there are alternate optimal solutions.Which optimal solution:
a.uses only one type of truck?
b.utilizes the minimum total number of trucks?
c.uses the same number of small and large trucks?
Solve the problem graphically and note there are alternate optimal solutions.Which optimal solution:
a.uses only one type of truck?
b.utilizes the minimum total number of trucks?
c.uses the same number of small and large trucks?
(Essay)
4.8/5  (43)
(43)
Solve the following linear program by the graphical method.
MAX 4X + 5Y
s.t.X + 3Y < 22
-X + Y < 4
Y < 6
2X - 5Y < 0
X,Y > 0
(Essay)
4.8/5  (30)
(30)
Find the complete optimal solution to this linear programming problem.
Min 5X + 6Y
s.t.3X + Y > 15
X + 2Y > 12
3X + 2Y > 24
X ,Y > 0
(Essay)
4.8/5  (28)
(28)
An optimal solution to a linear programming problem can be found at an extreme point of the feasible region for the problem.
(True/False)
4.8/5  (32)
(32)
Because the dual price represents the improvement in the value of the optimal solution per unit increase in right-hand-side,a dual price cannot be negative.
(True/False)
4.9/5  (46)
(46)
A range of optimality is applicable only if the other coefficient remains at its original value.
(True/False)
4.8/5  (31)
(31)
Find the complete optimal solution to this linear programming problem.
Max 2X + 3Y
s.t.4X + 9Y < 72
10X + 11Y < 110
17X + 9Y < 153
X ,Y > 0
(Essay)
4.8/5  (41)
(41)
Given the following linear program:
MIN 150X + 210Y
s.t.3.8X + 1.2Y > 22.8
Y > 6
Y < 15
45X + 30Y = 630
X,Y > 0
Solve the problem graphically.How many extreme points exist for this problem?
(Essay)
4.8/5  (34)
(34)
The Sanders Garden Shop mixes two types of grass seed into a blend.Each type of grass has been rated (per pound)according to its shade tolerance,ability to stand up to traffic,and drought resistance,as shown in the table.Type A seed costs $1 and Type B seed costs $2.If the blend needs to score at least 300 points for shade tolerance,400 points for traffic resistance,and 750 points for drought resistance,how many pounds of each seed should be in the blend? Which targets will be exceeded? How much will the blend cost?
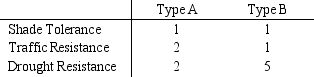
(Essay)
4.8/5  (23)
(23)
Showing 1 - 20 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)